![[Maple Plot]](images/F551.gif)
![[Maple Plot]](images/F551.gif)
| > | restart: |
| > | interface(showassumed=0):assume(h>0):assume(c>0):assume(a>0): |
| > | Nmax:=10: |
| > | n:=3: # число панелей 1-10 |
| > | for n to Nmax do |
| > | m3:=4*n+7:# Число узлов c опорами |
| > | n3:=8*n+8:# стержней фермы c опорами |
| > | m:=n3: |
| > | ns:=n3-3: |
| > | #a:=3: h:=4: |
| > | for i to 2*n+2 do x[i]:=a*i-a: y[i]:=0: x[i+2*n+2]:=a*i-a: y[i+2*n+2]:=h: od:#нижн |
| > | x[4*n+5]:=0: y[4*n+5]:=-1: |
| > | x[4*n+6]:=x[2*n+2]: y[4*n+6]:=-1: |
| > | x[4*n+7]:=x[2*n+2]+1: y[4*n+7]:=0: |
| > | #seq(y[i],i=1..m3); |
| > | Номер узла начала и конца стержня-вектора |
| > | for i to n+1 do |
| > | N[i]:=[i+1,i+2*n+2]; # кресты |
| > | N[i+n+1]:=[i+n,i+3*n+3]; # |
| > | od: |
| > | for i to 2*n+2 do |
| > | N[i+2*n+2]:=[i,i+2*n+2]; # stoyki |
| > | od: |
| > | for i to 2*n+1 do |
| > | N[i+4*n+4]:=[i+2*n+2,i+2*n+3]; # v poyas |
| > | od: |
| > | for i to n do |
| > | N[i+6*n+5]:=[i,i+1]; # n poyas |
| > | N[i+7*n+5]:=[i+n+1,i+n+2]; # n poyas |
| > | od: |
| > |
| > | N[n3-2]:=[1,m3-2]: N[n3-1]:=[2*n+2,m3-1]: # opors |
| > | N[n3]:=[2*n+2,m3]: |
| > |
Шрифт для номеров шарниров и стержней
| > | with(plots):with(plottools): |
| > | for i to m do R[i]:=PLOT(CURVES([[x[N[i][1]],y[N[i][1]]],[x[N[i][2]],y[N[i][2]]]])):od: |
| > | for i to m3+5 do Шарнир[i]:=PLOT(TEXT([x[i]+0.1,y[i]+0.1],convert(i,symbol)), COLOR(HUE,1)): od: |
| > | for i to m do Стержень[i]:=PLOT(TEXT([(x[N[i][1]]+2*x[N[i][2]])/3,(y[N[i][1]]+2*y[N[i][2]])/3+0.1],convert(i,symbol)), COLOR(HUE,0.7)):od: |
| > |
Изображение фермы
| > | #display(seq(Шарнир[i],i=1..m3),seq(R[i],i=1..m),seq(Стержень[i],i=1..m),scaling=unconstrained,axes=none); |
| > |
Заполнение матрицы
Правая часть системы - вектор нагрузок(фактически набор векторов - каждый столбец - одна нагрузка. Система решается сразу для всех случаев. См. Решебник Теор мех с.344)
| > | B1:=Vector(m): G:=Matrix(m,m): |
| > | np:=2;B1[2*np]:=-1: |
Решение системы
| > | for i to m do |
| > | Lxy[1]:=x[N[i][2]]-x[N[i][1]]: |
| > | Lxy[2]:=y[N[i][2]]-y[N[i][1]]: |
| > | L[i]:=subs(a^2+h^2=c^2,sqrt(Lxy[1]^2+Lxy[2]^2)); |
| > | for j to 2 do |
| > | jj:=2*N[i][2]-2+j: |
| > | if jj<=m then G[jj,i]:=-Lxy[j]/L[i]:fi; |
| > | jj:=2*N[i][1]-2+j: |
| > | if jj<=m then G[jj,i]:= Lxy[j]/L[i]:fi; |
| > | od; |
| > | od: |
| > | G1:=1/G: # Обратная матрица |
| > | S1:=G1.B1: # Решение системы |
| > | seq(S1[jj],jj=m-2..m); |
| > | #Прогиб |
| > |
| > | DEL:=simplify((C1*a^3+C2*c^3+C3*h^3));#должно совпасть с del |
| > |
| > | del:=simplify(add(S1[i]*S1[i]*L[i],i=1..ns)*h^2);# |
| > | C1[n]:=coeff(del,a^3); |
| > | C2[n]:=coeff(del,c^3); |
| > | C3[n]:=coeff(del,h^3); |
| > | print(del,n);od: |
| > |
| > |
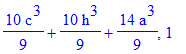
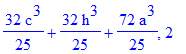
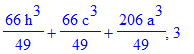
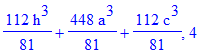
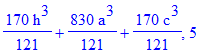
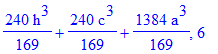
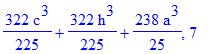
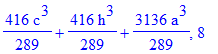
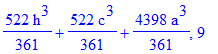
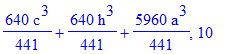
| > | n:='n':with(genfunc):#перед a^3 |
| > | S:=seq(C1[i]*(2*i+1)^2,i=1..Nmax); |
| > | NN:=nops([S])/2; |
| > | Z:=rgf_findrecur(NN, [S], t,n); |
![]()
![]()
![]()
| > | ZZ:=simplify(rsolve({Z,seq(t(i)=S[i],i=1..NN)},t)); |
![]()
| > |