Лекция 13. Графы

4.2. Связность

Маршруты

Рассматривая геометрический граф, можно зафиксировать некоторую вершину и, последовательно двигаясь по смежным ребрам, перейти в другую вершину или вернуться в исходную. Конечно, по ориентированному ребру перемещение допустимо только в направлении его ориентации. Последовательность ребер, по которым можно двигаться непрерывным образом, играют в теории графов фундаментальную роль.

Определение 4.9. Последовательность из  ребер графа (не обязательно различных) называется маршрутом длины , если любые два рядом стоящие в этой последовательности ребра смежные. Кроме того, если эти два рядом стоящие ребра ориентированные, то в инцидентную им вершину ребро, стоящее слева, должно входить, а ребро, стоящее справа, из нее выходить.

  Пусть маршрут задан ребрами  и ребру  соответствует пара вершин , где . Говорят, что маршрут замкнут, если , и не замкнут, если . Для не замкнутого маршрута вершина  называется начальной вершиной, а вершина   - конечной. В этом случае говорят, что маршрут соединяет вершины  и . Еще говорят, что вершина  связана с вершиной .

Любая вершина, инцидентная двум рядом стоящим ребрам маршрута, называется внутренней или промежуточной вершиной. Так как ребра и вершины в маршруте могут повторяться, то внутренняя вершина может также оказаться начальной или конечной вершиной.

  Маршрут неориентированного графа называют неориентированным маршрутом (составной цепью), а маршрут орграфа называют ориентированным маршрутом (составным путем). Если все ребра незамкнутого маршрута попарно различны, то такой маршрут неориентированного графа называется цепью, а орграфа - путем. Если попарно различны все вершины незамкнутого маршрута, то такой маршрут неориентированного графа называется простой цепью, а орграфа - простым путем. Если попарно различны все ребра замкнутого маршрута, то такой маршрут неориентированного графа называется циклом, а орграфа - контуром. Замкнутый маршрут, в котором попарно различны все вершины, кроме первой и последней, называется в неориентированном графе простым циклом, а в орграфе - простым контуром.

  Маршрут назовем нетривиальным, если он содержит хотя бы одно ребро; для систематичности рассуждений вводится еще нуль-маршрут, вообще не содержащий ребер, - этот маршрут состоит

только из одной вершины графа.

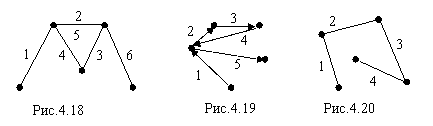
На рис.4.18 приведен пример составной цепи, на рис.4.19 приведен пример пути, а на рис.4.20 - пример простой цепи.

Связные компоненты

Пусть задан неориентированный граф. Граф называется связным, если любые две несовпадающие вершины графа соединены маршрутом. Очевидно, что для связности графа необходимо и достаточно, чтобы произвольная фиксированная вершина графа соединялась маршрутом с каждой из оставшихся вершин этого графа.

  Отношение связности рефлексивно (вершина всегда связана сама с собой), симметрично (из связности вершины  с вершиной  следует связность вершины  с вершиной ) и транзитивно (если вершины ,  и вершины ,  связаны, то связаны и вершины ,). Таким образом, отношение связности для вершин есть отношение эквивалентности. Поэтому существует такое разбиение множества вершин графа на попарно непересекающиеся подмножества (классы эквивалентности), что все вершины в каждом подмножестве связаны, а вершины из различных подмножеств не связаны. Каждое такое подмножество вершин графа вместе с ребрами, инцидентными этим вершинам, образует связный подграф. Следовательно, неориентированный граф представим единственным образом в виде объединения непересекающихся связных подграфов. Эти подграфы называют связными компонентами рассматриваемого графа. Связный граф является своей единственной компонентой связности. На рис.4.21 изображен граф, который имеет три компоненты связности.

  Теперь обратимся к ориентированному графу. Если в орграфе существует маршрут, связывающий вершины  и , то говорят, что вершина  достижима из вершины . Любая вершина считается достижимой из себя самой. Вершина орграфа называется источником, если из нее достижима любая вершина орграфа.

  Связность ориентированных графов определяется в принципе так же, как и неориентированных, те есть без учета направления дуг. Специфичным для орграфа (или смешанного графа) является понятие сильной связности.

Орграф называется сильным (или сильносвязным), если любые две его вершины достижимы друг из друга. Орграф называется односторонним (или одностороннесвязным), если для любой пары его вершин, по меньшей мере, одна из них достижима из другой.

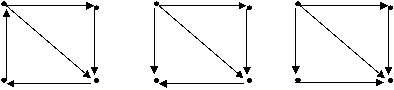
    Рис.4.22                           Рис.4.22                               Рис.4.22          

Орграф называется слабым (или слабосвязным), если связным графом является его неориентированный дубликат. На рис. 4.22 изображен сильный орграф, на рис. 4.23 - односторонний, а на рис. 4.23 - слабый. Поскольку вершина графа достижима из себя, то одновершинный орграф будет одновременно и сильным, и односторонним, и слабым. Каждый сильный орграф является односторонним, а каждый односторонний - слабым. Очевидно, что две любые несовпадающие вершины сильного орграфа принадлежат некоторому контуру.

  В некоторых задачах существенно требование сильной связности графа. Например, граф, представляющий план города с односторонним движением по некоторым улицам, должен быть сильно связанным, так как, в противном случае, нашлись бы вершины (площади и перекрестки), между которыми нельзя было бы проехать по городу без нарушения правил движения.

  Маршрут, содержащий все вершины орграфа, называется остовным.

Теорема 4.5. Орграф является сильным тогда и только тогда, когда в нем есть остовный контур, является односторонним тогда и только тогда, когда в нем есть остовный путь.

      Отношение взаимной достижимости вершин орграфа рефлексивно, симметрично и транзитивно. Как отношение эквивалентности оно разбивает множество вершин орграфа на классы эквивалентности, объединяя в один класс все вершины, достижимые друг из друга. Вершины, входящие в такие классы, вместе с дугами, им инцидентными, обе концевые вершины которых принадлежат этому же классу, образуют подграфы, называемые сильными (или сильносвязнными) компонентами орграфа.

      Орграф называется несвязным, когда его неориентированный дубликат не является связным графом.

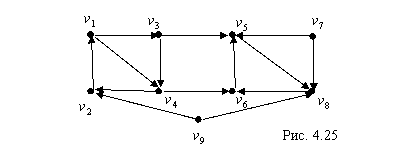
      Орграф, изображенный на рис. 4.25, имеет четыре сильные компоненты с множествами вершин , , , . В орграфе могут быть дуги, не входящие ни в одну из его сильных компонент, например, дуги , ,  и  у орграфа на рис. 4. 25.

Вершинная связность и реберная связность

      Сопоставляя, например, полный граф шестого порядка и его любой связный суграф, интуитивно ясно, что сам полный граф «сильнее» связан, чем его суграф. Далее речь пойдет о понятиях, характеризующих степень связности графа.

      Рассмотрим граф, вершины которого соответствуют неким технологическим объектам, а ребра показывают, какие объекты могут взаимодействовать либо непосредственно друг с другом, либо опосредованно через другие объекты. Технологическая система, представленная этим графом, считается функционирующей, если каждая пара ее объектов связана между собой. В этом случае система должна иметь связный граф. Важной характеристикой системы является ее надежность (живучесть), под которой обычно понимается способность системы функционировать при выходе из строя одного или нескольких объектов и (или) нарушения связи между некоторыми из них. Очевидно, что менее надежной следует считать ту систему, которая перестает функционировать при выходе из строя меньшего количества ее элементов. Оказывается, оценить степень надежности такой системы могут помочь те понятия, о которых упоминалось чуть выше и которые сейчас будут определены.

Определение 4.10. Числом вершинной связности (или просто числом связности)  графа  называется число, равное наименьшему числу вершин, удаление которых приводит к несвязному или одновершинному графу.

      Граф , представленный на рис. 4.26, связен, но он перестает быть связным, если удалить вершину 4. Поэтому .

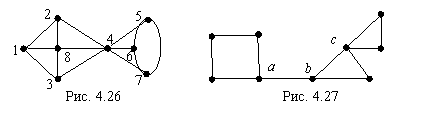
      Можно нарушить связность графа, удаляя некоторые его ребра (дуги). У графа  (рис. 4.26) для этого придется удалить не менее трех ребер. Например, граф  распадается на две компоненты после удаления ребер  4&5, 4&6, 4&7.

Определение 4.11. Числом реберной связности  графа  называется число, равное наименьшему числу ребер, удаление которых приводит к несвязному графу. Число реберной связности одновершинного графа полагается равным нулю.

      Выше мы показали, что для графа  (рис. 4.26) .

      Вершина  графа  называется точкой сочленения (разделяющей вершиной), если граф , полученный после операции удаления у графа  вершины , имеет больше компонент связности, чем сам граф . В частности, если  связен и  - точка сочленения, то  не связен.

      Ребро  графа  называется мостом, если его удаление увеличивает число компонент связности графа.

      Таким образом, точки сочленения и мосты - это своего рода «узкие места» графа.  Граф на рис. 4.27 имеет три точки сочленения - это вершины , , , и один мост - ребро .

      Возвращаясь к технологической системе, речь о которой шла вначале, отметим, что число вершинной связности и число реберной связности ее графа отражают чувствительность системы к повреждениям, а точки сочленения и мосты графа системы указывают на наиболее уязвимые места системы.

      Граф называется неразделимым, если он связный и не имеет точек сочленения. Граф, имеющий хотя бы одну точку сочленения, является разделимым и называется сепарабельным. Он разбивается на блоки, каждый из которых представляет собой максимальный неразделимый подграф.

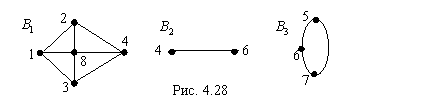
На рис. 4.28 показаны блоки , ,  графа на рис. 4.26.

      Если  есть минимальная степень вершин графа , то очевидно, что , поскольку удаление всех ребер, инцидентных данной вершине, приводит к увеличению числа компонент связности графа.

Теорема 4.6. Для любого графа  справедливы неравенства:

.

Граф  называется k-связным, если , реберно- k-связным, если .

      Граф , изображенный на рис. 4.26, 1-связен и реберно-3-связен.