Лекция 14. Графы
Расстояния
Пусть ![]() -
связный неориентированный граф. Так как любые две вершины графа
-
связный неориентированный граф. Так как любые две вершины графа ![]() и
и ![]() связаны, то существуют простые цепи
с концами
связаны, то существуют простые цепи
с концами ![]() и
и
![]() . Таких цепей
может быть несколько. Их длины являются неотрицательными целыми числами. Следовательно,
между вершинами
. Таких цепей
может быть несколько. Их длины являются неотрицательными целыми числами. Следовательно,
между вершинами ![]() и
и ![]() должны существовать простые цепи наименьшей
длины. Длина цепи наименьшей длины, связывающей вершины
должны существовать простые цепи наименьшей
длины. Длина цепи наименьшей длины, связывающей вершины ![]() и
и ![]() , обозначается символом
, обозначается символом ![]() и называется расстоянием
между вершинами
и называется расстоянием
между вершинами ![]() и
и
![]() . По определению
. По определению
![]() .
.
Нетрудно убедиться, что введенное таким образом понятие расстояния, удовлетворяет аксиомам метрики:
1. ![]() ;
;
2. ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() ;
;
3. ![]() ;
;
4. справедливо неравенство треугольника:
![]() .
.
Для фиксированной вершины графа ![]() расстояние до наиболее
удаленной от нее вершины:
расстояние до наиболее
удаленной от нее вершины: ![]() , называют
эксцентриситетом (максимальным удалением) вершины
, называют
эксцентриситетом (максимальным удалением) вершины ![]() .
.
Диаметром графа ![]() называют
число
называют
число ![]() , равное расстоянию между
наиболее удаленными друг от друга вершинами графа:
, равное расстоянию между
наиболее удаленными друг от друга вершинами графа:
![]() .
.
Простая цепь, длина которой равна ![]() , называется диаметральной
цепью. Очевидно, что диаметр графа равен наибольшему среди всех эксцентриситетов
вершин графа. Вершина
, называется диаметральной
цепью. Очевидно, что диаметр графа равен наибольшему среди всех эксцентриситетов
вершин графа. Вершина ![]() называется периферийной, если
называется периферийной, если ![]() .
.
Минимальный из эксцентриситетов вершин связного графа ![]() называют
его радиусом и обозначают
называют
его радиусом и обозначают ![]() :
:
![]() .
.
Так как диаметр графа равен наибольшему из эксцентриситетов
вершин, а радиус - наименьшему, то радиус графа не может быть больше его диаметра.
Вершина ![]() называется
центральной, если
называется
центральной, если ![]() . Множество всех центральных вершин графа называют
его центром. Центром графа может быть одна вершина или несколько вершин.
Есть графы, центр которых совпадает с множеством всех его вершин. Например,
центр простой цепи состоит из двух вершин при четном числе ее вершин и из одной
- при нечетном, а у любого цикла все
вершины являются центральными.
. Множество всех центральных вершин графа называют
его центром. Центром графа может быть одна вершина или несколько вершин.
Есть графы, центр которых совпадает с множеством всех его вершин. Например,
центр простой цепи состоит из двух вершин при четном числе ее вершин и из одной
- при нечетном, а у любого цикла все
вершины являются центральными.
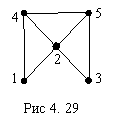 Для иллюстрации обратимся к графу на рис.
4.29. Здесь
Для иллюстрации обратимся к графу на рис.
4.29. Здесь
![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]()
![]() ,
, ![]() ,
,
![]()
![]() . Поэтому
. Поэтому
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Вершина 2 является центром графа, а все остальные его вершины - периферийные. Цепь 1, 2, 3 - одна из диаметральных цепей.
Для связного орграфа расстояние ![]() между вершинами
между вершинами ![]() и
и ![]() определяется как расстояние между
вершинами
определяется как расстояние между
вершинами ![]() и
и
![]() в неориентированном дубликате
этого графа.
в неориентированном дубликате
этого графа.
Задача нахождения центральных вершин графа постоянно встречается в практической деятельности. Пусть, например, вершины графа соответствуют небольшим поселкам, а его ребра - дорогам между ними. Требуется оптимально разместить по этим населенным пунктам, скажем, магазины. В подобных ситуациях критерий оптимальности обычно заключается в оптимизации «наихудшего» случая, то есть в минимизации расстояния от магазина до наиболее удаленного поселка. Такой подход к оптимизации предполагает размещение магазинов в поселках, которые представляют центральные вершины графа.
Обходы графов
Уже отмечалось, что начало теории графов связывают с задачей о кенигсбергских мостах. Эта знаменитая в свое время задача состоит в следующем. Семь мостов города Кенигсберга (ныне Калининграда) были расположены на реке Прегель так, как изображено на рис. 4.30. Задача состоит в том, чтобы, выйдя из дома, вернуться обратно, пройдя только один раз по каждому мосту.
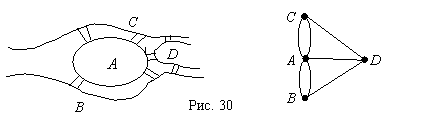
Так как в задаче существенны только переходы через мосты, план города
можно свести к изображению графа (точнее, мультиграфа), в котором ребра соответствуют
мостам, а вершины - различным разделенным
частям города, которые обозначены буквами ![]() (рис. 4.30, справа). Эйлер показал,
что нельзя пройти по одному разу по всем кенигсбергским мостам и вернуться назад.
В своей работе, опубликованной в 1736 году, он сформулировал и решил следующую
общую проблему теории графов: при каких условиях связный граф содержит цикл,
проходящий через каждое его ребро.
(рис. 4.30, справа). Эйлер показал,
что нельзя пройти по одному разу по всем кенигсбергским мостам и вернуться назад.
В своей работе, опубликованной в 1736 году, он сформулировал и решил следующую
общую проблему теории графов: при каких условиях связный граф содержит цикл,
проходящий через каждое его ребро.
 Цикл в графе называется эйлеровым,
если он содержит все ребра графа. Связный граф, в котором есть эйлеров цикл,
называется эйлеровым графом. Такой граф можно нарисовать, не отрывая
карандаша от бумаги и не повторяя линий.
Цикл в графе называется эйлеровым,
если он содержит все ребра графа. Связный граф, в котором есть эйлеров цикл,
называется эйлеровым графом. Такой граф можно нарисовать, не отрывая
карандаша от бумаги и не повторяя линий.
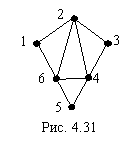
Например, граф, изображенный на рис. 4.31, является эйлеровым, поскольку он содержит эйлеров цикл 1, 2, 3, 4, 5, 6, 4, 2, 6, 1. В этом графе есть и другие эйлеровы циклы. Ясно, что любые два таких цикла отличаются друг от друга только порядком обхода ребер.
Теорема 4.7. (Л. Эйлер, 1736 г.) Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.
Цепь называется эйлеровой, если она содержит все ребра графа.
Теорема 4.8 (Л. Эйлер, 1736 г.) Мультиграф обладает эйлеровой цепью тогда и только тогда, когда он связен и число вершин нечетной степени равно 0 или 2.
Классическая интерпретация
задачи о гамильтоновых циклах -
задача о шахматном коне: можно ли, начиная из произвольного
поля на шахматной доске, ходить конем в такой последовательности, чтобы, пройдя
через каждое из шестидесяти четырех полей доски, вернуться в исходное положение.
Как практическую задачу, связанную с гамильтоновыми циклами, можно назвать известную
задачу о коммивояжере: коммивояжер должен побывать в каждом
из ![]() городов по одному разу,
выехав из одного из них и вернувшись в него же. При этом, зная расстояние между
любыми двумя городами, надо определить кратчайший маршрут, то есть требуется
найти в полном взвешенном графе гамильтонов цикл минимального веса.
городов по одному разу,
выехав из одного из них и вернувшись в него же. При этом, зная расстояние между
любыми двумя городами, надо определить кратчайший маршрут, то есть требуется
найти в полном взвешенном графе гамильтонов цикл минимального веса.
Несмотря на «похожесть» в определениях для эйлеровых и гамильтоновых циклов, соответствующие теории, устанавливающие критерии существования и алгоритмы поиска таких циклов, имеют мало общего. Терема Эйлера (теорема 4.7) позволяет легко установить, является ли граф эйлеровым. Разработаны алгоритмы, позволяющие достаточно просто найти эйлеровы циклы эйлерова графа. Что касается гамильтоновых графов, то здесь положение дел существенно иное. Ответить на вопрос, является ли некий граф гамильтоновым, как правило, очень трудно. Общего критерия, подобного критерию Эйлера, здесь нет. Но, как оказалось, среди множества всех графов эйлеровых графов ничтожно мало, а вот гамильтоновых графов достаточно много.