Элементы математической логики
Согласно общим представлениям логика есть область научных знаний, в которой исследуются различные способы суждений и умозаключений и анализируются наиболее общие законы и формы мышления. Математическая логика является частью так называемой формальной логики и изучает методы логических рассуждений с помощью математического аппарата и специального символьного исчисления. Хорошо известно, что математика рассматривает количественные отношения и формы, абстрагируясь от свойств конкретных материальных объектов. Точно так же и математическая логика анализирует, прежде всего, форму доводов (утверждений, понятий) в том или ином рассуждении, отвлекаясь от конкретного содержания этих доводов. Результаты этих исследований находят свое применение не только в "чистой" математике, но и в кибернетике, вычислительной технике, теории управления, различных технических науках, лингвистике, биологии, экономике.
Первые общие схемы (правила) рассуждений были изложены еще в древности греческим философом Аристотелем (384-322 г. до н.э.). Независимо от Аристотеля некоторыми схемами умозаключений занимались древнегреческие философы-стоики. Значительно позже определенный прогресс в логике наступил благодаря трудам философа и математика Г.В. Лейбница (1646-1716), который впервые высказал идею о введении в логику математических идей и символики. Однако эта идея Лейбница не была реализована при его жизни. И только со второй половины XIX и в XX веке, благодаря работам Дж. Буля (1815-1864), Г. Фреге (1848-1925) и других ученых, в логике начался период интенсивного развития, приведший к тому, что были созданы первые системы математической логики. Большой вклад в развитие логики внесли и русские ученые П.С. Порецкий (1846-1907), И.И. Жегалкин (1869-1947). В XX веке огромную роль в развитии математической логики сыграл Д. Гильберт (1862-1943), предложивший программу формализации математики, связанную с разработкой оснований самой математики. Наконец, в последние десятилетия XX века бурное развитие математической логики было обусловлено развитием теории алгоритмов и алгоритмических языков, теории автоматов, теории графов (С.К. Клини, А. Черч, А.А Марков, П.С. Новиков и многие другие).
Знакомство с основными понятиями математической логики мы начнем с элементарной математической логики - логики высказываний.
1. Высказывания и логические связки. Формулы логики высказываний
В повседневной речи мы выражаем ту или иную мысль с помощью различных предложений. Если абстрагироваться от содержательного смысла таких предложений, а рассматривать каждое предложение только с позиции истинности или ложности данного предложения, то мы придем к понятию высказывания.
Основные определения
В математической логике высказыванием
называется повествовательное предложение (утверждение, суждение), которое может
быть либо только истинным, либо только ложным. Высказывания будем обозначать
буквами латинского алфавита ![]() ,
, ![]() ,
, ![]() и т.д., которые назовем логическими
переменными (или пропозициональными переменными).
и т.д., которые назовем логическими
переменными (или пропозициональными переменными).
Пусть ![]() есть множество высказываний, а множество
есть множество высказываний, а множество ![]() состоит из двух
символов — 0 и 1 (
состоит из двух
символов — 0 и 1 (![]() ).
Установим отображение
).
Установим отображение ![]() так,
что каждому истинному высказыванию соответствует 1, а каждому ложному — 0.
Символы 1 и 0 назовем значениями истинности высказываний.
так,
что каждому истинному высказыванию соответствует 1, а каждому ложному — 0.
Символы 1 и 0 назовем значениями истинности высказываний.
Из простых высказываний можно с помощью некоторых стандартных связок образовать новые (составные) высказывания. Саму процедуру применения логических связок называют логическими операциями. Поскольку нас всегда будет интересовать не содержательный смысл высказывания, а только значение его истинности, для определения логических операций (связок) достаточно задать значение истинности результата применения логической операции. Такое значение истинности задается таблицей истинности логической операции.
Определение 1. Отрицанием высказывания ![]() называется
высказывание, соответствующее словам: «не
называется
высказывание, соответствующее словам: «не ![]() », «неверно, что
», «неверно, что ![]() ». Отрицание обозначается
символом
». Отрицание обозначается
символом ![]() или
┐
или
┐![]() и
задается таблицей истинности 1.
и
задается таблицей истинности 1.
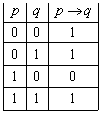
Табл. 1 Табл. 2
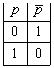
Отметим, что отрицание является унарной логической операцией.
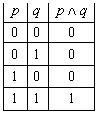
Определение 2. Конъюнкцией двух высказываний ![]() ,
,
![]() называют
третье высказывание
называют
третье высказывание ![]() (читается
«
(читается
«![]() и
и ![]() », другое обозначение
конъюнкции
», другое обозначение
конъюнкции ![]() &
&![]() ), которое истинно тогда
и только тогда, когда истинно
), которое истинно тогда
и только тогда, когда истинно ![]() и истинно
и истинно ![]() (табл. 2).
(табл. 2).
Конъюнкцию часто еще называют «логическим произведением» высказываний, поскольку таблица 2 по форме ничем не отличается от таблицы обычного произведения двух целых чисел — 0 и 1.
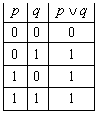
Определение 3. Дизъюнкцией двух высказываний ![]() ,
,
![]() называется
высказывание
называется
высказывание ![]() (читается
«
(читается
«![]() или
или ![]() »), которое ложно в том
и только в том случае, когда ложно
»), которое ложно в том
и только в том случае, когда ложно ![]() и ложно
и ложно ![]() (табл. 3).
(табл. 3).
В математической логике дизъюнкцию понимают
как союз «или», употребленный в неисключающем смысле слова[1].
Дизъюнкцию высказываний ![]() ,
, ![]() иногда называют «логической суммой»
высказываний. Последняя строка таблицы 3 отличает логическую сумму как от
традиционной суммы целых чисел, так и от сложения по модулю 2 (напомним, что
1+1=0(mod 2)).
иногда называют «логической суммой»
высказываний. Последняя строка таблицы 3 отличает логическую сумму как от
традиционной суммы целых чисел, так и от сложения по модулю 2 (напомним, что
1+1=0(mod 2)).
Табл. 4 Табл. 3