Элементы математической логики
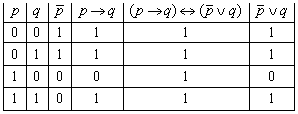
Пример 4. Составим таблицу истинности для формулы 
(табл.
6)
Табл. 6
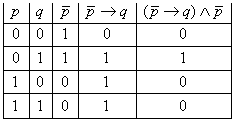
Пример 5. Формализовать высказывание: «если самолет вылетел согласно расписанию и по маршруту следования были хорошие метеоусловия, то самолет прилетает в аэропорт назначения по расписанию».
Перечислим следующие
высказывания: 
–
«самолет вылетел по расписанию», высказывание 
– «по маршруту следования были хорошие
метеоусловия», 
–
«самолет прилетает в аэропорт назначения по расписанию». Тогда исходное
высказывание можно записать в виде следующей логической формулы: 
.
Пример 6. Формализовать высказывание: «неверно, что число 100 делится на 11 и делится на 3».
Пусть есть высказывание «100 делится
на 11», –
высказывание «100 делится на 3». Исходное высказывание можно записать в виде 
.
Мы уже видели, что для
выяснения значения истинности любой формулы 
в эту формулу подставляют упорядоченный
набор значений истинности высказываний 
. Каждый такой конкретный набор значений
истинности (т.е. элемент множества 
, где 
) называется интерпретацией формулы 
.
Определение 7. Формула 
называется общезначимой
(или тавтологией), если она истинна в любой интерпретации.
Для обозначения общезначимой формулы используют
запись 
(тавтология
обозначается символом ö).
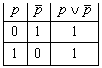
Пример 7. 
, что подтверждается таблицей 7.
Табл. 7
Определение 8. Формула называется противоречивой
(или контрадикцией), если она ложна в любой интерпретации. Для
обозначения противоречивой формулы используют запись 
.
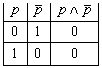
Пример 8. 
, что соответствует таблице 8.
Табл. 8
Используя тавтологию и контрадикцию, мы получаем
возможность оперировать формулами, содержащими символы 1 и 0 , — таковы,
например, формулы 
или
.
Определение 9. Формула называется выполнимой,
если она истинна не во всех интерпретациях.
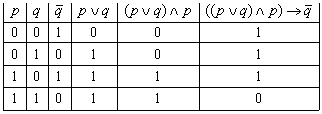
Пример 9. 
— выполнимая формула (табл. 9),
поскольку в интерпретации, когда истинно, истинно, эта формула является ложной.
Табл. 9
Определение 10. Формула 
логически следует из
формулы (запись
), если
формула 
имеет
значение «истина» во всех тех интерпретациях, при которых формула имеет значение
«истина».
Следующая теорема, которую мы приводим без доказательства, задает критерий справедливости логического следования.
Теорема 1. Формула логически следует из формулы в том и только в том
случае, когда импликация 
является общезначимой, т.е. 
.
Определение 11. Две формулы и 
называются логически эквивалентными
(или равносильными), если их эквиваленция есть тавтология при любых наборах
значений истинности высказываний 
, 
.
Для равносильных формул и обычно используют запись 
. Согласно определению
11, равносильность двух формул означает, что и одновременно 
.
Пример 10. 
. Две указанные формулы равносильны, так как
их эквиваленция 
есть
тавтология (табл. 10).
Нетрудно заметить, что две формулы являются равносильными, если их логические значения совпадают на любых одинаковых упорядоченных наборах значений истинности высказываний, входящих в состав формул (сравните четвертый и последний столбцы табл. 10).
Табл. 10
Отметим, наконец, что сама форма записи логических формул допускает существенные упрощения. Мы пока лишь условимся опускать внешние скобки в обозначениях формул. Другие возможные упрощения будут обсуждаться в следующем разделе.
Основные законы логики
Общезначимые формулы выполняют особую роль в математической логике, так как они отражают ее основные законы.
Для любых высказываний и справедливы следующие законы логики:
1) коммутативность дизъюнкции и конъюнкции:
, 
;
2) ассоциативность дизъюнкции и конъюнкции:
, 
;
3) законы дистрибутивности:
, 
;
4) законы идемпотентности:
, 
;
5) свойства «логических постоянных» 0 и 1:
, 
;
, 
;
,
;
6) закон двойного отрицания:
┐ (┐
)
или 
;
7) законы противоречия и исключенного третьего:
, 
;
8) законы 
Моргана
, 
.