Программа 25. Задача 42

>    restart;

>    with(PDEtools): declare(s(t),phi(t)):

>    read "C:\\diff.m";

>    read "C:\\teylor.m";

>    read "C:\\graph.m";

Обозначения

>    f:=phi(t): vs:=diff(s(t),t): w:=diff(f,t):

Известны скорости

>    v[P,1]:=0: v[P,2]:=0: v[B,1]:=vs:

>    G[1]:=Граф([P,B],[R],[Pi/2],[w1]):

>    G[2]:=Граф([A,B],[R-r],[f+Pi/2],[w]):

>    G[3]:=Граф([A,K,B],[r,R],[f-Pi/2,f+Pi/2],[w2,w1]):

>    k:=0:

>    for i to 3 do #Формируем систему

>     for j to 2 do k:=k+1: eq[k]:=G[i][j]

>    od;od;

>    #solve({G[1][1],G[2][1],G[2][2],G[3][2]},{v[A,1],v[A,2],w1,w2});

>    Система:=seq(eq[k],k=1..6);

s(t)*`will now be displayed as`*s

phi(t)*`will now be displayed as`*phi

`Система` := s[t] = -R*w1, v[B,2] = 0, s[t] = v[A,1]-(R-r)*cos(phi)*phi[t], v[B,2] = v[A,2]-(R-r)*sin(phi)*phi[t], s[t] = v[A,1]+r*cos(phi)*w2-R*cos(phi)*w1, v[B,2] = v[A,2]+r*sin(phi)*w2-R*sin(phi)*w1...

>    Решение:=solve({Система},{v[B,2],v[A,1],v[A,2],w1,w2});assign(Решение);

`Решение` := {v[B,2] = 0, w2 = (-phi[t]*R+phi[t]*r-s[t])/r, v[A,1] = s[t]+cos(phi)*phi[t]*R-cos(phi)*phi[t]*r, w1 = -s[t]/R, v[A,2] = sin(phi)*phi[t]*R-sin(phi)*phi[t]*r}

>    Va:=simplify(sqrt(v[A,1]^2+v[A,2]^2)):

>    J1:=m[1]*R^2:J2:=m[2]*r^2/2:

>    T:=collect(1/2*m[1]*vs^2+1/2*J1*w1^2+1/2*m[2]*Va^2+1/2*J2*w2^2,w,factor);

T := 3/4*m[2]*(-R+r)^2*phi[t]^2-1/2*s[t]*m[2]*(2*cos(phi)+1)*(-R+r)*phi[t]+1/4*s[t]^2*(4*m[1]+3*m[2])

>    P:=m[2]*g*(R-(R-r)*cos(f)):#Потенциальная энергия

>    L:=T-P:#Кинетический потенциал

Уравнения Лагранжа

>    Eq1:=collect(diff(Дифф(L,vs),t)-Дифф(L,s(t)),diff(w,t),factor);

Eq1 := -1/2*m[2]*(2*cos(phi)+1)*(-R+r)*phi[t,t]-m[2]*sin(phi)*phi[t]^2*R+m[2]*sin(phi)*phi[t]^2*r+2*s[t,t]*m[1]+3/2*s[t,t]*m[2]

>    Eq2:=factor(diff(Дифф(L,w),t)-Дифф(L,f));

Eq2 := 1/2*m[2]*(-R+r)*(3*phi[t,t]*r-s[t,t]-2*cos(phi)*s[t,t]-2*g*sin(phi)+2*s[t]*sin(phi)*phi[t]-3*phi[t,t]*R)

>    Order:=2:

>    U1:=Тейлор(Eq1,[diff(s(t),t,t),diff(w,t),phi(t)]);

>    U2:=simplify(Тейлор(Eq2,[diff(s(t),t,t),diff(w,t),phi(t)])/m[2]/(R-r));

U1 := (2*m[1]+3/2*m[2])*s[t,t]-3/2*m[2]*(-R+r)*phi[t,t]

U2 := 3/2*s[t,t]-3/2*phi[t,t]*r+3/2*phi[t,t]*R+g*phi

>    Реш:=solve({U1,U2},{diff(w,t),diff(s(t),t,t)});

`Реш` := {phi[t,t] = 1/6*g*phi*(4*m[1]+3*m[2])/m[1]/(-R+r), s[t,t] = 1/2*m[2]*g*phi/m[1]}

>    -rhs(Реш[1])/f;

-1/6*g*(4*m[1]+3*m[2])/m[1]/(-R+r)

>    k:=sqrt(%);#Частота колебаний

k := 1/6*(-6*g*(4*m[1]+3*m[2])/m[1]/(-R+r))^(1/2)

>    limit(k,m[1]=infinity);

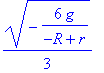
1/3*(-6*g/(-R+r))^(1/2)

>