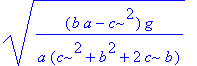Программа 28. Задача 46. Паллограф

>

restart;

>	read "C:\\diff.m";

>	read "C:\\teylor.m";

>	read "C:\\graph.m";  assume(phi(t)<Pi/6,phi(t)>0,c>0);

>	interface(showassumed=0):

>	with(PDEtools): declare(phi(t)):

>	v[O,1],v[O,2],v[B,1]:=0$3:# Условия на скорости

>	psi(t):=arccos((a/c)*sin(phi(t))):

>	w1:=diff(phi(t),t):       # Угловая скорость 1

>	G1:=Граф([O,A,B],[a,c],[Pi/2+phi(t),psi(t)],[w1,w2]):

>	w2:=simplify(solve(G1[1],w2)):# Угловая скорость 2

>	G2:=Граф([O,A,C],[a,b],[Pi/2+phi(t),Pi+psi(t)],[w1,w2]):

>	Решение:=solve({G2[1],G2[2]},{v[C,1],v[C,2]}):

>	assign(Решение):

>	Vc:=sqrt(v[C,1]^2+v[C,2]^2):  # Скорость C

>	T:=simplify(m*Vc^2/2):        # Кинетическая энергия

>	Q:=expand((-m*g*v[C,2])/w1):  # Обобщенная сила

Уравнение Лагранжа 2-го рода

>	eq:=simplify(diff(Дифф(T,diff(phi(t),t)),t)-Дифф(T,phi(t))-Q):

>

Order:=2:

Линеаризация

>	Eq:=collect(Тейлор(eq,[diff(phi(t),t$2),diff(phi(t),t),phi(t)]),phi(t),factor);

>	sqrt(-solve(Eq,diff(phi(t),t$2))/phi(t));# Частота