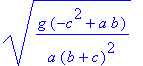Программа 29. Задача 46

 Паллограф, с. 123, 387

>    restart;

>    read "C:\\diff.m";

>    read "C:\\teylor.m";

>    read "C:\\graph.m";

>    with(PDEtools):

>    declare(phi(t),psi(t),alpha(t),y(t)):

>    y1:=diff(y(t),t):# Скорость ползуна

>    v[B,1]:=0:v[B,2]:=y1:

>    G:=Граф([C,B],[b+c],[psi(t)],[w2]);

phi(t)*`will now be displayed as`*phi

psi(t)*`will now be displayed as`*psi

alpha(t)*`will now be displayed as`*alpha

y(t)*`will now be displayed as`*y

G := [0 = v[C,1]-(b+c)*sin(psi)*w2, y[t] = v[C,2]+(b+c)*cos(psi)*w2]

>    Решение:=solve({G[1],G[2]},{v[C,1],v[C,2]}):

>    assign(Решение);

>    Vc:=sqrt(v[C,1]^2+v[C,2]^2):#Скорость С

>    T:=simplify(m*Vc^2/2); # Кинетическая энергия

T := 1/2*m*(w2^2*b^2+2*w2^2*b*c+w2^2*c^2+y[t]^2-2*y[t]*cos(psi)*w2*b-2*y[t]*cos(psi)*w2*c)

>    eq[4]:=a*cos(phi(t))+c*sin(psi(t))-y(t):# f1 связь

>    eq[5]:=a*sin(phi(t))-c*cos(psi(t)):     # f2 связь

>    N:=-m*g*v[C,2]:  # Мощность

>    Q[1]:=diff(N,w1):# Обобщенные силы

>    Q[2]:=diff(N,w2):

>    Q[3]:=Дифф(N,y1):

>    T:=subs(w2=diff(psi(t),t),T):

>    q:=[phi(t),psi(t),y(t)]:

>    for i to 3 do # Уравнения Лагранжа

>     eq[i]:=diff(Дифф(T,diff(q[i],t)),t)-Дифф(T,q[i])-Q[i]-lambda[1]*Дифф(eq[4],q[i])-lambda[2]*Дифф(eq[5],q[i]);

>    od:

>    psi(t):=Pi/2-alpha(t):

>    Order:=2:

>    z:=diff(alpha(t),t$2),diff(alpha(t),t),alpha(t),diff(phi(t),t$2),diff(phi(t),t),phi(t),y1:

>    for i to 5 do # Линеаризуем

>     Eq[i]:=Тейлор(eq[i],[z]);

>    od;

Eq[1] := -lambda[2]*a+lambda[1]*a*phi

Eq[2] := -lambda[2]*c+1/2*m*(-2*b^2-4*c*b-2*c^2)*alpha[t,t]+(-lambda[1]*c+m*g*(-b-c))*alpha

Eq[3] := m*g+lambda[1]

Eq[4] := a+c-y

Eq[5] := a*phi-c*alpha

>    alpha(t):=solve(Eq[5],alpha(t));

>    Z:=eliminate({seq(Eq[i],i=1..3)},{lambda[1],lambda[2]}):

alpha := a*phi/c

>    factor(sqrt(-solve(op(Z[2]),diff(phi(t),t$2))/phi(t))); #Частота

(g*(-c^2+a*b)/a/(b+c)^2)^(1/2)