Программа 47.  Статически неопределимая рама

>

restart:

>	read "C:\\epura.m";

>	read "C:\\Risepura.m";

>	read "C:\\Podpr1.m";

Ввод данных

>	fd := fopen("C:/M13/p65.txt",READ):# Открываем файл (SoprM-G.txt,p65, p65a.txt, p65d.txt, StrMech.txt,SoprM-S.txt)

>	x:=[parse(readline(fd))]:# x

>	y:=[parse(readline(fd))]:# y

>	n:=nops(x):   #Число узлов

>	P1:=[parse(readline(fd))]:#Нагрузки в узлах

>	P2:=[parse(readline(fd))]:#

>	P3:=[parse(readline(fd))]:#

>	str:=[parse(readline(fd))]:#Стержни. Номера узлов

>	m:=nops(str):              # Число стержней

>	Vns:=[parse(readline(fd))]: #

>	U:=[parse(readline(fd))]:   # Номер элемента множества Vns

>	OPOR:=[parse(readline(fd))]:# Опоры

>	Qx:=[parse(readline(fd))]:# Распределенная нагрузка

>	Qy:=[parse(readline(fd))]:# Распределенная нагрузка

>	EJ:=[parse(readline(fd))]:;# Относительная жесткость

>	Nms:=[parse(readline(fd))]:# Неизвестные метода сил[Узел, направление (1-X, 2-Y, 3-M)]

>	fclose(fd):                # Закрываем файл

>	ks:=nops(Vns):             # Число внутренних шарниров

>	Vns1:=Vector(n):

>	nv:=nops(U):              # Число внутренних неизвестных

>	ko:=nops(OPOR):           # Число опор

>	printf("Число  неизвестных  %d + %d, уравнений %d + %d + %d",ko,6*m,ks,3*m,3*n);

>	no:=nops(Nms): # Число внешних неизвестных

>	nn:=no+nv:     # Общее число  неизвестных

  Решение

>

Lxy():

>	RisRama();

Число  неизвестных  3 + 18, уравнений 0 + 9 + 12

>	EpuraM(P1,P2,P3):#Моменты в основной системе

>	Реакции=seq(Ro[i],i=1..ko);

>	RQ(Rx,Ry):       #Поперечная сила в осн.сист.

>	PrintRez(Q1,"Qp");

 N    Qp(1)     Qp(2) 

1   24.00    0.00  

2    6.00    6.00  

3    0.00    0.00  

>	QP:=Matrix(m,2,Q1):

>	RisEpur(QP,'QP',0);

>	MP:=Matrix(m,2,Rm):

>	RisEpur(MP,'MP',1);

>	PrintRez(Rm,"Mp");

>	Qx0:=Qx:  Qy0:=Qy: #Сохраняем данные(распр.нагр)

 N    Mp(1)     Mp(2) 

1   60.00  -24.00  

2   24.00    0.00  

3    0.00    0.00  

>	for j to no do

>	P1:=Vector(n):P2:=Vector(n):P3:=Vector(n): #Обнуляем нагрузки

>	Qx:=Vector(m):Qy:=Vector(m):

>	z:=Nms[j,2]:

>	P||z[Nms[j,1]]:=1:           #Прикладываем единичную нагрузку

>	EpuraM(P1,P2,P3):

>	m||j:=Matrix(m,2,Rm):

>	RisEpur(m||j,cat("m",j),1);

>	RQ(Rx,Ry):

>	q||j:=Matrix(m,2,Q1):

>	RisEpur(q||j,cat("q",j),0);

>

od:

>	for j to nv do

>	P1,P2,P3:=Vector(n)$3: #Обнуляем нагрузки

>	Qx,Qy:=Vector(m)$2:

>	Vns1:=Vector(n):

>	Vns1[U[j]]:=1;    #Прикладываем единичную нагрузку

>	EpuraM(P1,P2,P3):j1:=j+no:

>	m||j1:=Matrix(m,2,Rm):

>	RisEpur(m||j1,cat("m",j1),1);

>	RQ(Rx,Ry):

>	q||j1:=Matrix(m,2,Q1):

>	RisEpur(q||j1,cat("q",j1),0);

>

od:

>	for j to nn do

>	PrintRez(m||j,cat("m",j));

>	PrintRez(q||j,cat("q",j));

>	Эпюраq||j;

>	Эпюраm||j;

>

od;

 N    m1(1)     m1(2) 

1    3.00    0.00  

2    0.00    0.00  

3    0.00    0.00  

 N    q1(1)     q1(2) 

1    1.00    1.00  

2    0.00    0.00  

3    0.00    0.00  

 N    m2(1)     m2(2) 

1   -6.00    6.00  

2   -6.00    2.00  

3   -2.00    0.00  

 N    q2(1)     q2(2) 

1    0.00    0.00  

2   -1.00   -1.00  

3   -1.00   -1.00  

>	Deltap:=Vector(nn): delta:=Matrix(nn):

>	for i to nn do

>	Deltap[i]:=evalf(add(int(EM(MP,1,u,k)*EM(m||i,0,u,k)/EJ[k],u=0..L[k]),k=1..m));

>	for j to nn do

>	delta[i,j]:=evalf(add(int(EM(m||i,0,u,k)*EM(m||j,0,u,k)/EJ[k],u=0..L[k]),k=1..m));

>

od:

>

od:

Решаем систему канонических уравнений

>	X:=-delta^(-1).Deltap:

>	delta,X,Deltap;#Коэфф.канонических уравнений, неизвестные

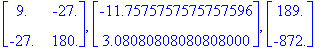
Моменты в статически неопр. раме

>	MR:=add(m||i*X[i],i=1..nn)+MP:

Поперечные силы в статически неопр. раме  

>	QR:=add(q||i*X[i],i=1..nn)+QP:

>	PrintRez(QR,`Q`);

>	Qx:=Qx0: Qy:=Qy0: #Восстанавливаем нагрузки

 N    Q(1)     Q(2) 

1   12.24  -11.76  

2    2.92    2.92  

3   -3.08   -3.08  

>	PrintRez(MR,`M`);

 N    M(1)     M(2) 

1    6.24   -5.52  

2    5.52    6.16  

3   -6.16    0.00  

>	RisEpur(MR,`M`,1);

>	RisEpur(QR,`Q`,0);