Программа 52. Задача 70.
| > | restart; |
Процедура дифференцирования по t любого порядка
| > | Dif:=proc(x,i) if i=0 then x else diff(x,t$i) fi end: |
| > | with(LinearAlgebra): |
| > | with(PDEtools,declare): declare(x(t)): |
Максимальный порядок
| > | Nmax:=3: N:=Nmax-2: A:=Matrix(N+1): |
Исcледуемое уравнение
| > | eq:=16*diff(x(t),t$2)*sqrt(diff(x(t),t))+b*diff(x(t),t)+x(t)^4; |
Производные уравнения по времени порядка от 0 до N
| > | for k from 0 to N do z[k+1]:=Dif(eq,k);od: |
Задаем порядок особой точки и скорость
| > | Порядок:={0,3}; v0:=1: |
![eq := 16*t*x[t,t]*x[t]^(1/2)+b*x[t]+x^4](images/P522.gif){kind=small}
Порядок искомых производных (для уравнения 2 порядка)
| > | SET:={seq(j,j=0..Nmax)} minus Порядок; |
Заполнение матрицы
| > | for i to N+1 do |
| > | for j to N+1 do |
| > | A[i,j]:=subs(xx=Dif(x(t),SET[j]), |
| > | diff(subs(Dif(x(t),SET[j])=xx,z[i]),xx)); |
| > | od: |
| > | od: |
| > | A; |
Условие нестабильности
| > | Dtr:=Determinant(A); |
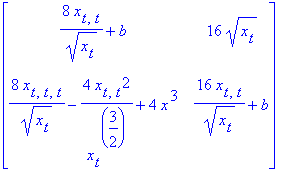
![Dtr := 1/x[t]*(192*x[t,t]^2+24*x[t,t]*b*x[t]^(1/2)+b^2*x[t]-128*x[t,t,t]*x[t]-64*x^3*x[t]^(3/2))](images/P526.gif)
Выражение 2-й производной функции из уравнения (необходимо, если в Dtr входит 2-я производная)
| > | xtt:=solve(eq,diff(x(t),t$2)); |
| > | xttt:=diff(xtt,t); |
![xtt := -1/16*(b*x[t]+x^4)/x[t]^(1/2)](images/P527.gif)
![xttt := -1/16*(b*x[t,t]+4*x^3*x[t])/x[t]^(1/2)+1/32*(b*x[t]+x^4)/x[t]^(3/2)*x[t,t]](images/P528.gif)
Подстановка 2-й и 3-й производной функции в условие нестабильности
| > | Dtr1:=simplify(subs(diff(x(t),t$3)=xttt,Dtr)); |
| > | Dtr2:=collect(simplify(subs(diff(x(t),t$2)=xtt,Dtr1)),x(t)); |
![Dtr1 := 1/x[t]^(3/2)*(192*x[t,t]^2*x[t]^(1/2)+28*x[t,t]*b*x[t]+b^2*x[t]^(3/2)-32*x[t]^2*x^3-4*x[t,t]*x^4)](images/P529.gif)
![Dtr2 := 1/x[t]^2*x^8-32*x[t]^(1/2)*x^3](images/P5210.gif)
| > | subs(diff(x(t),t)=v0,Dtr2); |
| > |
| > | _MaxSols:=4; |
| > | evalf(solve(subs(diff(x(t),t)=v0,Dtr2),x(t))); |
