Программа 53. Задача 71. Определение условия нестабильности системы 2 уравнений
restart;
Процедура дифференцирования по t любого порядка
| > | Dif:=proc(x,i) if i=0 then x else diff(x,t$i) fi end: |
| > | with(LinearAlgebra): x1:=X(t): x2:=Y(t): |
| > | with(PDEtools,declare): declare(x1,x2): |
Исследуемая система уравнения
| > | eq[1]:=diff(x1,t$2)*(x1^2+3*x2)+2*x1*x2+diff(x1,t)*(2*x1+3*x2); |
| > | eq[2]:=diff(x1,t$2)*x1+7*diff(x2,t$2)*x1+4*x1+3*x2; |
![eq[1] := X[t,t]*(X^2+3*Y)+2*X*Y+X[t]*(2*X+3*Y)](images/P533.gif){kind=small}
![eq[2] := X[t,t]*X+7*Y[t,t]*X+4*X+3*Y](images/P534.gif){kind=small}
Выражение ускорений из системы уравнений
| > | EQ:=subs(diff(x1,t$2)=xtt,diff(x2,t$2)=ytt,{eq[1],eq[2]}): |
| > | assign(solve(EQ,{xtt,ytt})); |
Процедура нахождения условия нестабильности с подстановкой ускорений(xtt,ytt) из уравнений движения
| > | NC:=proc(M) local i,j,Dtr;global A; |
| > | A:=Matrix(2): |
| > | for i to 2 do |
| > | for j to 2 do |
| > | A[i,j]:=subs(xx=Dif(x||j,M),diff(subs(Dif(x||j,M)=xx,eq[i]),xx)); |
| > | od: |
| > | od: |
Dtr:=simplify(Determinant(A));
collect(numer(simplify(subs({diff(x1,t$2)=xtt,diff(x2,t$2)=ytt},Dtr))),X(t));
| > | end proc: |
Условие нестабильности с учетом значений скоростей
| > | U0:=subs(diff(x1,t)=1,diff(x2,t)=0,NC(0)); |
| > | A; # Матрица исследуемой системы |
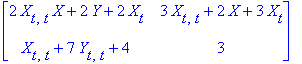
| > | with(plots): |
| > | W0:=subs(x1=X1,x2=Y1,U0): |
| > | implicitplot(W0,X1=-1..1,Y1=-1..1,numpoints=2000); |
| > | solve(W0,Y1); |
| > |