Программа 55. Задача 73. Устойчивость при ползучести

>

restart;

>	N:=2:   # Порядок особой точки

>	U:=u(t):# Прогиб

>	P:=p(t):# Деформация ползучести

>	with(PDEtools):

>	declare(prime=t,u(t),p(t)):#Штрих- произв по времени

>	eq1:=diff(U,t)+U*diff(P,t)*(alpha/P-lambda):  # Уравнение прогиба

>	ur1:=diff(P,t)*P^alpha=c:                     # Соотношение ползучести

>	s1:=seq(diff(eq1,t$i),i=1..N-1):              # Продифф уравнения

>	s2:=seq(diff(ur1,t$i),i=1..N-1):              # Продифф соотношение ползучести

>	z1:=seq(diff(p(t),t$N+1-i)=Д||i,i=1..N-1):    # Обозначения для производных деф.ползучести

>	z2:=seq(Д||i,i=1..N-1):                       # Список производных деф.ползучести

>	z3:=seq(diff(u(t),t$N+1-i)=w||(N+1-i),i=1..N):# Обознач для производных прогиба

>	z4:=seq(w||i,i=0..N-1):                       # Список производных прогиба в системе

>	syst:=subs(z1,{eq1,s1,s2}):                   # Полная система уравнений

>	eq5:=eliminate(%,{z2}):                       # Исключаем производные деф.ползучести

>	syst:=op(eq5)[2]:

>	S1:=subs(z3,u(t)=w0,syst):

>	S2:=subs(lambda=xi/P,S1):

>	solve(S2,{z4});

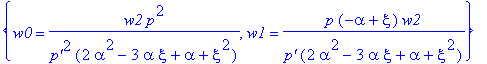
>	eq:=collect(denom(rhs(%[1])),xi,factor);

>	with(LinearAlgebra):

>	A:=GenerateMatrix(S2,[z4]);

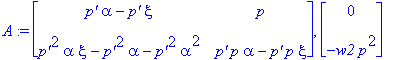
>	map(factor,A[1]);

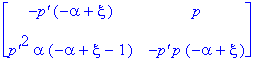
>	#Determinant(A[1]);

>	solve(eq,xi);#Особая точка

>
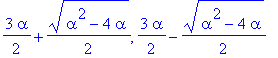