|
Тренировочные задачи региональной олимпиады Статика
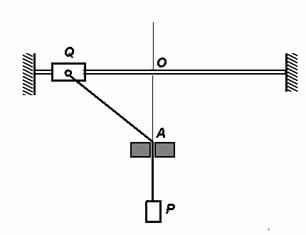
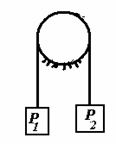
Три одинаковых шара положены на горизонтальную плоскость, взаимно прикасаются и обвязаны шнуром, огибающим их в экваториальной плоскости. Четвертый точно такой же шар лежит на трёх нижних. Масса каждого шара равна 1 кг. Пренебрегая силами трения, найти натяжение шнура.
|
 |
Задача 5
Водило ОС длиной L вращается вокруг
вертикальной оси с постоянной угловой скоростью ω. 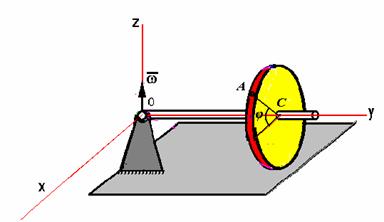 На водило насажен тонкий диск радиуса R, который
катится без скольжения по горизонтальной плоскости. Определить угол между
осестремительным и вращательным ускорением точки А на окружности диска. Положение
точки А определяется углом φ.
На водило насажен тонкий диск радиуса R, который
катится без скольжения по горизонтальной плоскости. Определить угол между
осестремительным и вращательным ускорением точки А на окружности диска. Положение
точки А определяется углом φ.
Задача 6
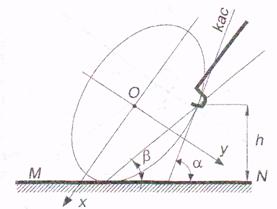 Мальчик бежит с постоянной скоростью
V и с помощью водила катит перед собой обод, имеющий форму эллипса
с полуосями а и b (а > b). Точка касания водила с ободом находится на постоянной высоте h над землей. Выразить угловую скорость w обода, катящегося без проскальзывания, как
функцию углов a, и b.
Мальчик бежит с постоянной скоростью
V и с помощью водила катит перед собой обод, имеющий форму эллипса
с полуосями а и b (а > b). Точка касания водила с ободом находится на постоянной высоте h над землей. Выразить угловую скорость w обода, катящегося без проскальзывания, как
функцию углов a, и b.
Задача 7
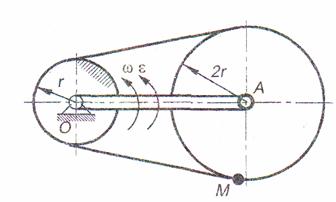 Кривошип ОА длины L вращается с угловой скоростью w и угловым ускорением e вокруг оси О неподвижной шестеренки
и несет на конце А ось другой шестеренки. Шестеренки охватываются цепью.
Найти скорость и ускорение точки М подвижной шестеренки в тот момент,
когда АМ ^ ОА .
Кривошип ОА длины L вращается с угловой скоростью w и угловым ускорением e вокруг оси О неподвижной шестеренки
и несет на конце А ось другой шестеренки. Шестеренки охватываются цепью.
Найти скорость и ускорение точки М подвижной шестеренки в тот момент,
когда АМ ^ ОА .
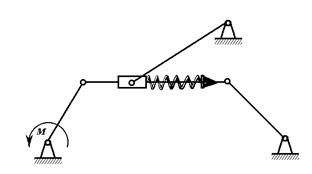
Задача 8
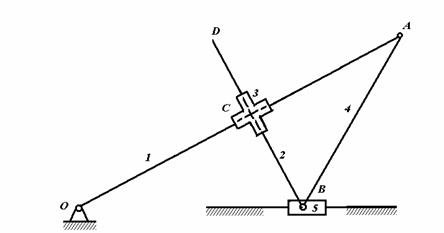
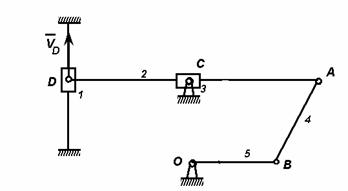 Для механизма, изображенного на рисунке, зная постоянную
скорость первого звена, определить угловое ускорение пятого звена. Геометрические
размеры выбрать самостоятельно.
Для механизма, изображенного на рисунке, зная постоянную
скорость первого звена, определить угловое ускорение пятого звена. Геометрические
размеры выбрать самостоятельно.
Задача 9
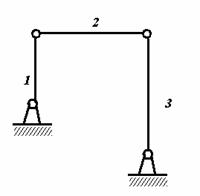 Для шарнирного четырехзвенника найти угловое ускорение
третьего звена при условии, что первое звено вращается с постоянной угловой
скоростью.
Для шарнирного четырехзвенника найти угловое ускорение
третьего звена при условии, что первое звено вращается с постоянной угловой
скоростью.
Задача 10
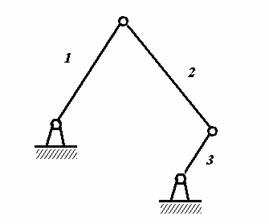 Для шарнирного четырехзвенника найти угловое ускорение
третьего звена при условие, что первое звено вращается с постоянной угловой
скоростью. Геометрические размеры задать самостоятельно. Первое и третье звенья
параллельны, угол между первым и вторым не равен 900.
Для шарнирного четырехзвенника найти угловое ускорение
третьего звена при условие, что первое звено вращается с постоянной угловой
скоростью. Геометрические размеры задать самостоятельно. Первое и третье звенья
параллельны, угол между первым и вторым не равен 900.
Задача 11
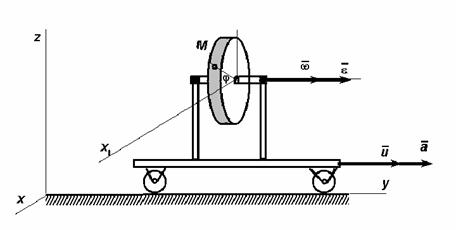 Тележка движется со скоростью
Тележка движется со скоростью ![]() и
ускорением
и
ускорением ![]() . Диск радиуса R, установленный на тележке вращается
с угловой скоростью
. Диск радиуса R, установленный на тележке вращается
с угловой скоростью ![]() и
угловым ускорением
и
угловым ускорением ![]() .
Положение точки М в данный момент времени определяется углом j. Определить проекции ускорения
точки М на координатные оси при j = 2700.
.
Положение точки М в данный момент времени определяется углом j. Определить проекции ускорения
точки М на координатные оси при j = 2700.
Задача 11
 На рис. изображен двухстепенной гироскоп в кардановом
подвесе. Угловая скорость рамки равна
ω1, радиус
диска OM равен R. Заданные угловые скорости постоянны по абсолютной величине.
Положение точки М в данный момент времени
определяется углом j. Найти проекции абсолютного ускорения точки М на координатные
оси при j = 0.
На рис. изображен двухстепенной гироскоп в кардановом
подвесе. Угловая скорость рамки равна
ω1, радиус
диска OM равен R. Заданные угловые скорости постоянны по абсолютной величине.
Положение точки М в данный момент времени
определяется углом j. Найти проекции абсолютного ускорения точки М на координатные
оси при j = 0.
Задача 12
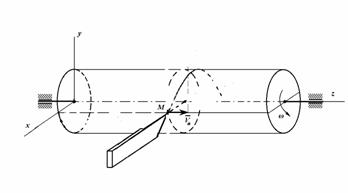 Резец движется поступательно с постоянной скоростью
Резец движется поступательно с постоянной скоростью ![]() . Определить радиус кривизны
траектории точки М резца относительно цилиндра, вращающегося равномерно с
угловой скоростью w
вокруг неподвижной оси oz.
. Определить радиус кривизны
траектории точки М резца относительно цилиндра, вращающегося равномерно с
угловой скоростью w
вокруг неподвижной оси oz.
Динамика
Задача 1
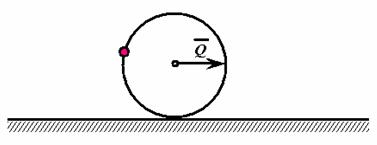 Однородный диск радиусом R и массой m1 c укрепленной
на его окружности точечной массой m1 катится без скольжения по горизонтальной плоскости.
К диску приложена горизонтальная сила Q, как показано на рисунке. Составить
дифференциальное уравнение движения.
Однородный диск радиусом R и массой m1 c укрепленной
на его окружности точечной массой m1 катится без скольжения по горизонтальной плоскости.
К диску приложена горизонтальная сила Q, как показано на рисунке. Составить
дифференциальное уравнение движения.
Задача 2
 Тележка весом Р на колесах радиуса R установлена
на наклонной плоскости под углом φ к горизонту. Какова должна быть мощность тягача, чтобы
везти тележку вверх по наклонной плоскости со скоростью V. Коэффициент
трения скольжения – f , коэффициент трения качения
– δ.
Тележка весом Р на колесах радиуса R установлена
на наклонной плоскости под углом φ к горизонту. Какова должна быть мощность тягача, чтобы
везти тележку вверх по наклонной плоскости со скоростью V. Коэффициент
трения скольжения – f , коэффициент трения качения
– δ.
Задача 3
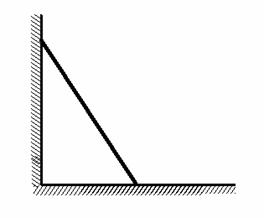 Однородный стержень длиной L опирается на гладкую стену и гладкий пол. В начальный
момент образует угол j0 с вертикалью.
Составить дифференциальные уравнения движения. Учесть, что с течением времени
изменяется число степеней свободы стержня.
Однородный стержень длиной L опирается на гладкую стену и гладкий пол. В начальный
момент образует угол j0 с вертикалью.
Составить дифференциальные уравнения движения. Учесть, что с течением времени
изменяется число степеней свободы стержня.
Задача 4
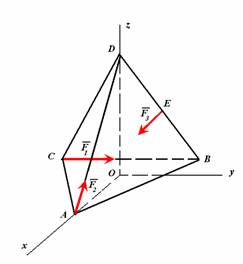
 Прямоугольный треугольник с катетами a и b вращается
вокруг катета b. Определить
координаты приложения равнодействующей сил инерции треугольника
Прямоугольный треугольник с катетами a и b вращается
вокруг катета b. Определить
координаты приложения равнодействующей сил инерции треугольника
 Задача 5
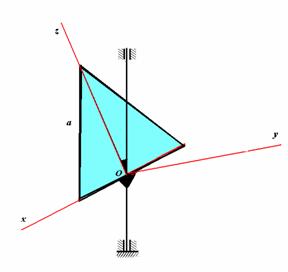
Задача 5
Правильный треугольник массой m и стороной a вращается с постоянной угловой скоростью w вокруг вертикальной оси под углом 600 к плоскости треугольника. Определить величину, направление и точку приложения равнодействующей сил инерции треугольника
Задача 6
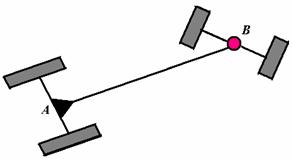
На рисунке изображена четырехскатная тележка. Передние колеса являются управляемыми. Составить уравнения связей и определить число степеней свободы.
Задача 7
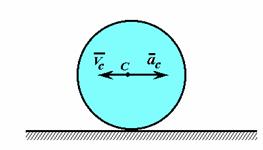
По бильярдному шару наносится центральный удар. Скорость центра масс шара после удара равна u . Радиус шара равен R, момент инерции относительно диаметра равен 2/5 mR2 . Определить максимальную угловую скорость шара и интервал времени, спустя который шар покатится без скольжения
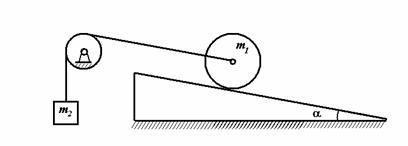
Задача 8
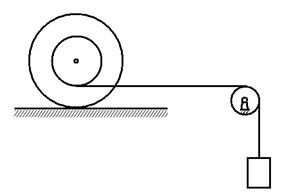 Система, изображённая на рисунке, состоит
из катушки массой m1, радиусами
R и r и радиусом инерции r и груза массой m2. Катушка
катится по плоскости со скольжением. Коэффициент трения скольжения равен f,
коэффициент трения качения – d. Массу неподвижного блока не учитывать.
Система, изображённая на рисунке, состоит
из катушки массой m1, радиусами
R и r и радиусом инерции r и груза массой m2. Катушка
катится по плоскости со скольжением. Коэффициент трения скольжения равен f,
коэффициент трения качения – d. Массу неподвижного блока не учитывать.
Задача 9
 Балка опирается одним концом на горизонтальную плоскость
и удерживается в наклонном положении с помощью верёвки. Коэффициент трения
между балкой и плоскостью f = 1. Какой угол должна балка составлять с горизонтом,
чтобы не скользить в момент обрыва веревки. Балку считать сплошным однородным
стержнем.
Балка опирается одним концом на горизонтальную плоскость
и удерживается в наклонном положении с помощью верёвки. Коэффициент трения
между балкой и плоскостью f = 1. Какой угол должна балка составлять с горизонтом,
чтобы не скользить в момент обрыва веревки. Балку считать сплошным однородным
стержнем.
Задача 10
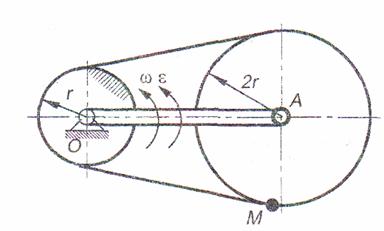 Кривошип ОА длины L и массой m1 вращается с угловой скоростью w вокруг оси О неподвижной шестеренки
радиусом r и несет на конце А ось другой шестеренки
радиусов 2 r. Шестеренки охватываются цепью. Найти скорость
и ускорение точки М подвижной шестеренки в тот момент, когда АМ ^ ОА.
Кривошип ОА длины L и массой m1 вращается с угловой скоростью w вокруг оси О неподвижной шестеренки
радиусом r и несет на конце А ось другой шестеренки
радиусов 2 r. Шестеренки охватываются цепью. Найти скорость
и ускорение точки М подвижной шестеренки в тот момент, когда АМ ^ ОА.
Задача 11
На рисунке изображен гироскоп с двумя степенями свободы.
Угловая скорость собственного вращения гироскопа равна ![]() , а угловая скорость прецессии
-
, а угловая скорость прецессии
-![]() . На величины
угловых скоростей никаких ограничений не налагается. Осевой момент инерции
гироскопа равен
. На величины
угловых скоростей никаких ограничений не налагается. Осевой момент инерции
гироскопа равен ![]() .
. ![]() . Определить реакции подшипников.
. Определить реакции подшипников.
Решение.
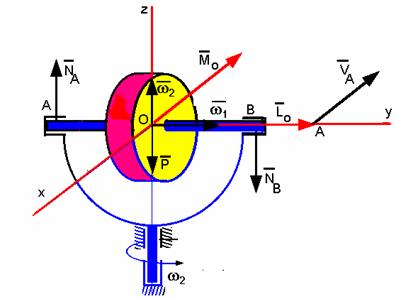 Для решения задачи применяем теорему
Резаля, согласно которой скорость конца вектора кинетического момента гироскопа
равна главному моменту всех сил относительно неподвижной точки. В рассматриваемом
случае угол между векторами угловых скоростей прецессии и собственного вращения
(угол нутации) равен 900 и поэтому применима теорема Резаля.
Для решения задачи применяем теорему
Резаля, согласно которой скорость конца вектора кинетического момента гироскопа
равна главному моменту всех сил относительно неподвижной точки. В рассматриваемом
случае угол между векторами угловых скоростей прецессии и собственного вращения
(угол нутации) равен 900 и поэтому применима теорема Резаля.
В соответствии с этим считаем, что кинетический момент гироскопа определяется как
![]()
и направлен вдоль оси собственного вращения гироскопа. В действительности кинетический момент по данной формуле не определяется, но при определении гироскопических реакций это не имеет значения.
Скорость конца вектора кинетического момента
![]()
Направления указанных
векторов указано на рисунке. По направлению скорости точки А направлен главный
момент всех сил относительно начала координат. Соответственно этому на рисунке
показаны направления реакций в подшипниках ![]() и
и ![]() .
.
Главный момент
![]() .
.
Следовательно
![]()
По теореме о движении центра масс гироскопа
![]()
После решения системы уравнений
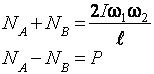 .
.
Находим реакции подшипников
![]() ,
,
![]()
Полученные реакции имеют статические и динамические составляющие. Момент гироскопических реакций приложен к гироскопу и может быть представлен так
![]()
По третьему закону Ньютона на подшипники со стороны гироскопа действует момент
![]() ,
,
который называется гироскопическим моментом.
Задача 12
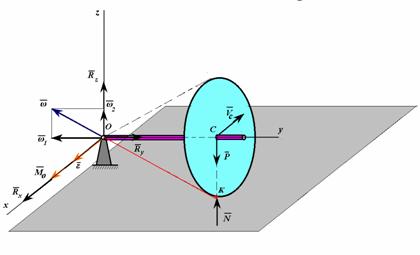 Тонкий однородный диск массой m радиусом R катится без скольжения по горизонтальной плоскости и
приводится в движение с помощью водила ОС, вращающегося с постоянной угловой
скоростью
Тонкий однородный диск массой m радиусом R катится без скольжения по горизонтальной плоскости и
приводится в движение с помощью водила ОС, вращающегося с постоянной угловой
скоростью ![]() вокруг
вертикальной на шаровом шарнире. Длина водила
вокруг
вертикальной на шаровом шарнире. Длина водила ![]() . Определить нормальную реакцию плоскости
и реакцию шаровой опоры, пренебрегая массой водила.
. Определить нормальную реакцию плоскости
и реакцию шаровой опоры, пренебрегая массой водила.
Решение.
Диск и водило
рассматриваем, как одно твердое тело с одной степенью свободы и назовем его
гироскопом. Начало координат выбираем в неподвижной точке О и связываем систему
координат Oxyz
с гироскопом. Точка К является для гироскопа мгновенным центром скоростей,
так как качение диска по плоскости происходит без скольжения. Точка О неподвижна
в любой момент времени. Следовательно, прямая ОК является мгновенной осью
вращения, вдоль которой направлен вектор абсолютной угловой скорости гироскопа.
Угловая скорость ![]() называется
угловой скоростью прецессии, угловая скорость
называется
угловой скоростью прецессии, угловая скорость ![]() называется угловой скоростью собственного
вращения.
называется угловой скоростью собственного
вращения.
Из соотношения
![]()
находим
![]()
![]() Так как угловые скорости постоянны по величине,
то угловое ускорение гироскопа
Так как угловые скорости постоянны по величине,
то угловое ускорение гироскопа
![]()
направлено по оси Ох и его величина
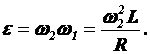 (1)
(1)
Далее рассмотрим,
какие силы действуют на гироскоп. Это сила тяжести Р, нормальная реакция N и реакции шаровой
опоры Rx, Ry, Rz. Предполагая, что нормальная реакция плоскости больше
силы тяжести, изобразим на рисунке главный момент ![]() всех сил относительно неподвижной точки.
всех сил относительно неподвижной точки.
Так как проекции углового ускорения гироскопа на оси Оz и Оу равны нулю, то для решения задачи достаточно использовать только одно из динамических уравнений Эйлера:
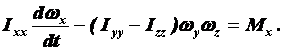 (2)
(2)
Учитывая, что
![]()
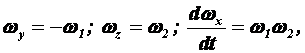
получим
![]() (3)
(3)
![]() Момент инерции
Момент инерции
 (4)
(4)
Величина главного момента
![]() (5)
(5)
После подстановки получим

или
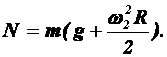 (6)
(6)
Для определения реакции шаровой опоры используем теорему
о движении центра масс. Центр масс гироскопа (массой водила пренебрегаем)
движется по окружности радиуса L. Угловая скорость
водила ![]() задана.
Ускорение центра масс
задана.
Ускорение центра масс![]() направлено, как указано на рис. 8 и его величина определяется по формуле
направлено, как указано на рис. 8 и его величина определяется по формуле
![]()
Запишем теорему о движении центра масс в проекции на ось Оу:
![]()
В проекциях на другие оси все силы уравновешены. Следовательно
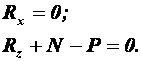
Таким образом
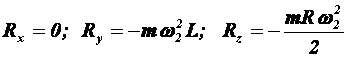 (7)
(7)
Студентам предлагается решить эту задачу самостоятельно с использованием теоремы Резаля.
Задача 13
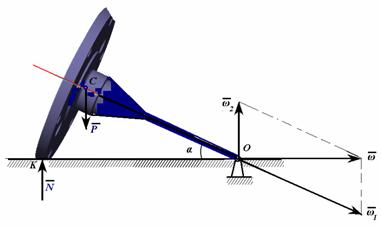
Диск массой m и радиуса R катится без скольжения по внутренней поверхности конуса. Приводится в движение с помощью водила длиной L, которое вращается вокруг вертикальной оси с постоянной угловой скоростью ω2. Определить нормальную реакцию конической поверхности.
Решение.
Рассмотрим построение кинематической схемы. Сначала изображаем диск и водило под углом к вертикали и проводим ось Oz1. Задаемся тоской К контакта диска с конусом. Через точку К проводим линию параллельно оси диска Oz до пересечения с неподвижной осью Oz1 и получаем таким образом вершину S конуса. Через вершину конуса проводим симметрично вторую образующую и затем изображаем основание конуса. Далее, вырезаем кусок конической поверхности, чтобы она не заслоняла диск с водилом. Строим неподвижную систему координат Ox1y1z1 и подвижную Oxyz. Через оси Ox и Oy проводим плоскость, пересечение которой с плоскостью Ox1y1 определяет линию узлов ON. Из углов Эйлера обозначим только угол нутации θ. Другие углы Эйлера не потребуются.
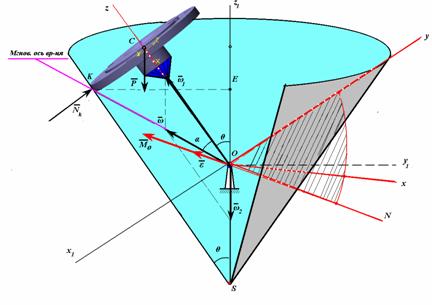 Прямая, проходящая через точки О и К есть мгновенная
ось вращения. Строим вектор угловой скорости прецессии, а затем строим параллелограмм
угловых скоростей. Угол между осью Oz и ОК обозначим через α.
Далее изобразим силы и приступаем к решению задачи.
Прямая, проходящая через точки О и К есть мгновенная
ось вращения. Строим вектор угловой скорости прецессии, а затем строим параллелограмм
угловых скоростей. Угол между осью Oz и ОК обозначим через α.
Далее изобразим силы и приступаем к решению задачи.
Найдем угловую скорость ω1 собственного вращения диска. Она определяется из условия
![]()
Из треугольника ОКС
![]() .
.
Отсюда находим
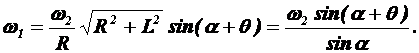
Так как угловые скорости ω1 и ω2, то угловое ускорение
![]()
направлено по линии узлов, как указано на рисунке. Так же направлен и главный момент всех сил относительно неподвижной точки. Движение диска представляет собой регулярную прецессию, следовательно
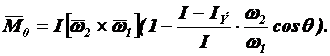
В данной задаче угол между угловыми скоростями равен
![]() . В соответствии с этим
. В соответствии с этим
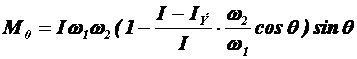 .
.
С другой стороны
![]()
Далее после элементарных преобразований получим
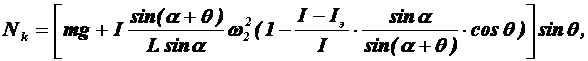
где
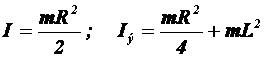 .
.
Полагая ![]() получаем
получаем
![]()
Задача 14
Коническое колесо, которое можно рассматривать, как тонкий диск массой m и радиуса R катится без скольжения по горизонтальной плоскости. Приводится в движение с помощью водила длиной L, которое вращается вокруг вертикальной оси с постоянной угловой скоростью ω2. Определить нормальную реакцию конической поверхности.
 Решение.
Решение.
Данная задача является частным случаем задачи №13. На рисунке построены все необходимые элементы. Мгновенная ось вращения расположена на прямой ОК.
Для решения задачи достаточно положить ![]() , а момент нормальной
реакции изменить в соответствии с рисунком.
, а момент нормальной
реакции изменить в соответствии с рисунком.
После простых преобразований получим
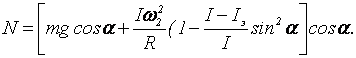
Окончательно
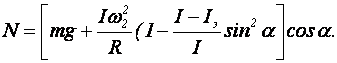


 На веревке,
обмотанной вокруг неподвижного цилиндра радиусом 0,2 м на 1,5 оборота, висит
груз весом 10 кН. Коэффициент трения между веревкой и цилиндром равен 0,8.
В каких пределах может изменяться вес груза, подвешенного к другому концу
веревки, в положении равновесия.
На веревке,
обмотанной вокруг неподвижного цилиндра радиусом 0,2 м на 1,5 оборота, висит
груз весом 10 кН. Коэффициент трения между веревкой и цилиндром равен 0,8.
В каких пределах может изменяться вес груза, подвешенного к другому концу
веревки, в положении равновесия.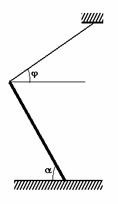

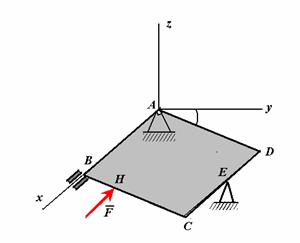
 Ползун
может скользить по двум направляющим. Между ползуном и направляющими имеется
малый зазор. Расстояние между направляющими равно Н. Длина ползуна равна а.
К ползуну приложена горизонтальная сила Р на расстоянии
Ползун
может скользить по двум направляющим. Между ползуном и направляющими имеется
малый зазор. Расстояние между направляющими равно Н. Длина ползуна равна а.
К ползуну приложена горизонтальная сила Р на расстоянии