Стабильность

Определение условия нестабильности системы с 2 степенями свободы

> restart;

Процедура дифференцирования по t любого порядка

> Dif:=proc(x,i) if i=0 then x else diff(x,t$i) fi end:

> with(LinearAlgebra):x1:=X(t):x2:=Y(t):

> with(PDEtools,declare):declare(x1,x2):

> A:=Matrix(2):

Исследуемое уравнение

> eq[1]:=diff(x1,t$2)+a*diff(x2,t)*x1+b*diff(x1,t)^2*x2^2+x1^2*diff(x2,t);

> eq[2]:=diff(x2,t$2)+c*diff(x1,t)+d*diff(x2,t)^2;

Порядок искомых производных (для уравнения 2 порядка)

> M:=1:

Заполнение матрицы

> for i to 2 do

> for j to 2 do

> A[i,j]:=subs(xx=Dif(x||j,M),diff(subs(Dif(x||j,M)=xx,eq[i]),xx));

> od:

> A;

Условие нестабильности

> Dtr:=Determinant(A);

> a:=1:b:=1:c:=1:d:=1:

> ur1:=subs(diff(x1,t)=1,diff(x2,t)=2,x1=U,x2=V,Dtr);

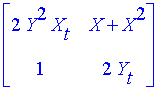
Matrix(%id = 13613436)

> with(geometry):

Warning, the previous binding of the name CrossProduct has been removed and it now has an assigned value

> conic(gr1,ur1=0,[U,V]);

detail(gr1);

$`name of the object: gr1\nform of the object: hyperbola2d\ncenter: [-1/2, 0]\nfoci: [[-1/2-3/8*2^(1/2), 0], [-1/2+3/8*2^(1/2), 0]]\nvertices: [[-1, 0], [0, 0]]\nthe asymptotes: [1/4*2^(1/2)*U+V+1...$
$`name of the object: gr1\nform of the object: hyperbola2d\ncenter: [-1/2, 0]\nfoci: [[-1/2-3/8*2^(1/2), 0], [-1/2+3/8*2^(1/2), 0]]\nvertices: [[-1, 0], [0, 0]]\nthe asymptotes: [1/4*2^(1/2)*U+V+1...$
$`name of the object: gr1\nform of the object: hyperbola2d\ncenter: [-1/2, 0]\nfoci: [[-1/2-3/8*2^(1/2), 0], [-1/2+3/8*2^(1/2), 0]]\nvertices: [[-1, 0], [0, 0]]\nthe asymptotes: [1/4*2^(1/2)*U+V+1...$
$`name of the object: gr1\nform of the object: hyperbola2d\ncenter: [-1/2, 0]\nfoci: [[-1/2-3/8*2^(1/2), 0], [-1/2+3/8*2^(1/2), 0]]\nvertices: [[-1, 0], [0, 0]]\nthe asymptotes: [1/4*2^(1/2)*U+V+1...$
$`name of the object: gr1\nform of the object: hyperbola2d\ncenter: [-1/2, 0]\nfoci: [[-1/2-3/8*2^(1/2), 0], [-1/2+3/8*2^(1/2), 0]]\nvertices: [[-1, 0], [0, 0]]\nthe asymptotes: [1/4*2^(1/2)*U+V+1...$
$`name of the object: gr1\nform of the object: hyperbola2d\ncenter: [-1/2, 0]\nfoci: [[-1/2-3/8*2^(1/2), 0], [-1/2+3/8*2^(1/2), 0]]\nvertices: [[-1, 0], [0, 0]]\nthe asymptotes: [1/4*2^(1/2)*U+V+1...$
$`name of the object: gr1\nform of the object: hyperbola2d\ncenter: [-1/2, 0]\nfoci: [[-1/2-3/8*2^(1/2), 0], [-1/2+3/8*2^(1/2), 0]]\nvertices: [[-1, 0], [0, 0]]\nthe asymptotes: [1/4*2^(1/2)*U+V+1...$

> coordinates(center(gr1));

> map(Equation,asymptotes(gr1));

> coordinates(vertices(gr1)[1]);

> coordinates(foci(gr1)[1]);

> draw(gr1);

[-1/2, 0]

[-1/2-3/8*2^(1/2), 0]

[Maple Plot]