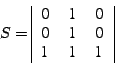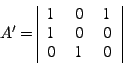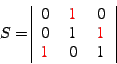|
Задача о назначениях
Стоимость производства детали
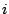 на станке на станке 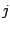 определяется коэффициентом определяется коэффициентом 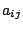 . Найти одно из оптимальных распределений станков и суммарную стоимость
производства. . Найти одно из оптимальных распределений станков и суммарную стоимость
производства.
Решение
Воспользуемся алгоритмом Куна (венгерским алгоритмом).
1. Преобразуем матрицу весов. Вычтем из каждой строки
минимальный элемент. В каждой строке появится по одному нулю
Если в каком-либо столбце не оказалось ни одного нуля,
с ним надо проделать такую же процедуру как и со строками:
найти минимальный элемент и вычесть его из этого столбца.
В данном случае таких столбцов нет
2. По преобразованной матрице весов 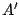 построим матрицу смежности двудольного графа построим матрицу смежности двудольного графа 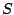 , так, что , так, что 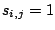 , если , если 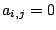 и и 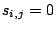 , если , если 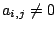 . Получим . Получим
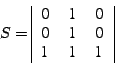
3. Находим наибольшее паросочетание полученного
двудольного графа 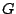 . Для этого можно воспользоваться алгоритмом
Форда-Фалкерсона. Изображаем граф (рис. 1) и одно (любое)
из его наибольших паросочетаний (рис. 2) . Для этого можно воспользоваться алгоритмом
Форда-Фалкерсона. Изображаем граф (рис. 1) и одно (любое)
из его наибольших паросочетаний (рис. 2)
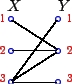
Рис. 1
|
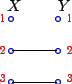
Рис. 2
|
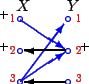
Рис. 3
|
Образуем множества ненасыщенных паросочетанием 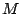 вершин
вершин
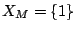 , , 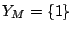 .
Если эти множества пустые, то задача решена, найдено
оптимальное решение. Из графа .
Если эти множества пустые, то задача решена, найдено
оптимальное решение. Из графа 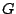 составим орграф,
в котором дуги, входящие в паросочетание составим орграф,
в котором дуги, входящие в паросочетание 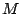 , направим от , направим от 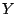 к к
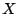 , а остальные дуги от , а остальные дуги от 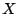 к к 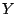 (рис. 3). (рис. 3).
Найдем вершины, достижимые из множества 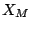 .
Эти вершины образуют два множества .
Эти вершины образуют два множества 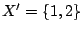 и и 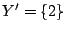 (на рис. 3 помечены +).
В соответствии с номерами (на рис. 3 помечены +).
В соответствии с номерами 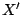 находим минимальный
элемент в строках 1,2 и столбцах находим минимальный
элемент в строках 1,2 и столбцах
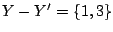 матрицы матрицы 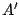 . Это . Это 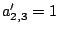 .
Вычитаем 1 из строк .
Вычитаем 1 из строк 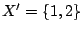 и добавляем 1 к столбцу и добавляем 1 к столбцу
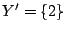
Возвращаемся к п. 2.
2'. Находим матрицу смежности двудольного графа
3'. Находим наибольшее паросочетание полученного
двудольного графа. Очевидно, паросочетание состоит из элементов
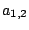 , , 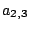 , , 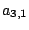 , с общим весом
4+2+2=8. Это и есть минимальная стоимость работы. , с общим весом
4+2+2=8. Это и есть минимальная стоимость работы.
Кирсанов М.Н. 2004
Опечатки исправил Седов А.
Задачи и решения по методу Куна см.
Кирсанов М.Н.
Графы в Maple
- М.:ФИЗМАТЛИТ, 2007.

|
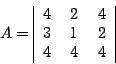
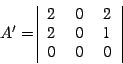
![]() построим матрицу смежности двудольного графа
построим матрицу смежности двудольного графа ![]() , так, что
, так, что ![]() , если
, если ![]() и
и ![]() , если
, если ![]() . Получим
. Получим