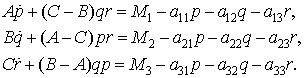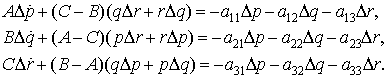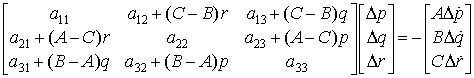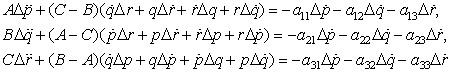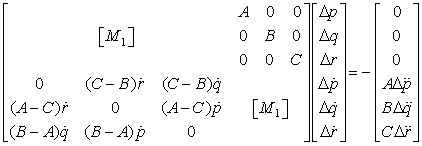СТАБИЛЬНОСТЬ СФЕРИЧЕСКОГО ДВИЖЕНИЯ

М.Н.Кирсанов

(Москва, Московский энергетический институт (ТУ), Россия)

        Решение задач механики предполагает следующую классическую схему: явление  →  модель  →  дифференциальное уравнение модели → решение уравнения  → анализ решения. При этом обычно предполагается, что решение уравнения описывает все свойства данной модели явления, следующие из уравнения. Того, чего нет в решении, того нет и в модели. Если результаты исследований не сходятся с практическим опытом, то исследователь уточняет или даже меняет модель или уточняет решение. Последнее бывает чаще, так как точных аналитических решений сложных уравнений, как правило, нет, и приходится прибегать к численному анализу, а там бесконечное поле деятельности для всякого рода уточнений.

         Если, например, изучается поведение какой-либо тонкостенной конструкции (явление — потеря несущей способности), то для анализа напряженно-деформированного  состояния привлекаются уравнения равновесия оболочек. Полученные решения дают условия исчерпания несущей способности по предельному состоянию, в частности при достижении условия пластичности. Если же практика расходится с теоретическими результатами, то исследователь начинает задумываться о возможности потери устойчивости конструкции (меняется модель). Привлекаются другие уравнения, полученные с учетом малых отклонений оболочки от основного процесса деформирования, и определяются условия выпучивания.

       Однако,  как это ни печально констатировать, самым тщательным образом рассчитанные модели, учитывающие все тонкости явления, не дают стопроцентной гарантии работоспособности системы. Колонны зданий (тщательно рассчитанные!) самым неожиданным  образом рушатся, самолеты падают, а ракеты взрываются. Что приводит их к этому? Это непонятно, так как все мыслимые и немыслимые расчеты сделаны, проверены и перепроверены!  Напрашивается вывод, что есть еще что-то такое, что исследователь не ввел в расчет. Цель этой работы — обосновать гипотезу, что белые пятна  не в указанной цепочке (явление  → … →  анализ решения), а вне ее. В этой цепочке есть неисследованная боковая ветвь: дифференциальное уравнение модели → свойства самого уравнения. Это направление не исследовалось, так как обычно предполагается (повторимся!), что решение уравнения описывает все то, что может дать данное уравнение явления.  Возможно, уравнение имеет какие-либо свойства, содержащие механический смысл. Обоснование этого тезиса проведем на модели сферического движения твердого тела.

          Рассмотрим движение твердого тела, имеющего неподвижную точку под действием моментов, зависящих от угловых скоростей. Уравнения движения имеют вид

                                                                (1)

Здесь  — проекции вектора угловой  скорости на подвижные оси координат , являющиеся главными осями инерции;   ,  — моменты инерции. Моменты , которые в общем случае могут являться функциями времени, будем трактовать как активные моменты от действия, например, внешних двигателей, а независящие от времени коэффициенты  считать характеристиками вязкого сопротивления среды. В данной задаче сопротивление принимается линейным. Пусть в результате некоторого процесса угловые скорости и ускорения получили  малые приращения:   , ,   , . Вариация (1) дает систему дифференциальных уравнений для приращений

                                              (2)

Поставим для системы (2) обобщенную задачу Коши. Обобщенная задача Коши отличается в данном случае тем, что на порядок производных, входящих в начальные условия, сняты ограничения. Зададим в начальных условиях значения производных , , . Для того, чтобы вычислить соответствующие значения функций и свести обобщенную задачу к классической, придется выразить величины , , через их скорости, решив систему (2) как линейную алгебраическую. В тех случаях, когда определитель системы обращается в нуль, появляются особые точки обобщенной задачи Коши. Ранее особые точки обобщенной задачи Коши находились в задаче выпучивания центрально сжатого стержня из реологического материала [1] и для движения кулисного механизма с одной степенью свободы [2]. Наличие особых точек в системе означает всякие критические ситуации, вызванные неопределенностью приращений функций процесса при как угодно малых возмущениях скоростей, ускорений или высших производных. Порядок возмущенных производных соответствует порядку особых точек. Условие отсутствия особых точек будем называть условием стабильности (constancy) процесса.  

             Найдем особые точки первого порядка. Запишем систему в матричном виде, отнеся в правую часть заданные скорости. Матрица системы имеет вид

         .                  (3)

Рассмотрим частный случай , . Приравнивая определитель системы (3) к нулю, получим условие возникновения нестабильной точки первого порядка

                                                                                    (4)

В случае Ковалевской  третье уравнение системы (1) имеет вид

                              .                                                                          (5)

 Это уравнение интегрируется. Для нулевых начальных данных  имеем решение

                                .                                                      (6)

Подставляя это решение в  (4), имеющее в этом случае простой вид                           ,   где коэффициент  характеризует вязкость, найдем критическое время   . Решение существует при . При исчезающе малой вязкости  критическое время стремится к величине  .

        Найдем условие нестабильности второго порядка. Продифференцируем по времени и проварьируем динамические уравнения Эйлера (1)

                                 (7)

Систему (2-7),  запишем в матричном виде

                                     (8)

Матрица (8) имеет клеточную структуру. Здесь     — матрица системы (3). Приравнивая к нулю определитель этой системы, получим условие нестабильности второго порядка

                                             (9)

Интересно проанализировать случай совпадения двух особых точек. Совместно с условием нестабильности первого порядка  (7) из (9) следует

                                    .

Учитывая уравнение движения (5), получим значение угловой скорости

                              .

Зная зависимость r  от времени (6), найдем критическое время

При исчезающе малой вязкости , критическое время стремится к величине .

                                               ЛИТЕРАТУРА

1.     Kirsanov M.N. Singular Points Of The Creep Deformation And Buckling Of A Column//International  Journal Eng.Science, 1997,V5,N3, pp. 221-227.

2.     Кирсанов М.Н. Возмущение ускорений и высших производных нелинейного динамического процесса. – Докл. межд. конф. «Информационные средства и технологии». Т.3 — М.: Янус-К, 2003, 64-66.

М.Н.Кирсанов

(Москва, Московский энергетический институт (ТУ), Россия)

СТАБИЛЬНОСТЬ СФЕРИЧЕСКОГО ДВИЖЕНИЯ

        При исследовании сферического движения твердого тела под действием моментов, зависящих от угловых скоростей, обнаружено новое механическое явление, связанное со свойствами дифференциального уравнения, описывающего движение. При некоторых условиях как угодно малые возмущения производных функций процесса приводят к неопределенным (или бесконечно большим)  приращениям функций или их производных. Вводится термин  - стабильность.  Обнаружены точки потери стабильности первого и второго порядка. Найдены условия совпадения этих точек. 

M.N.Kirsanov

(Moscow, the Moscow power institute (TU), Russia)

CONSTANCY OF SPHERICAL MOVEMENT

       At research of spherical movement of a rigid body under action of the moments dependent on angular speeds, the new mechanical phenomenon connected to properties of the differential equation, describing movement is revealed. Under some conditions somehow small indignations of derivative functions of process result to uncertain (or indefinitely big) to increments of functions or their derivatives. The term - constancy is entered. Points of loss of constancy of the first and second order are found out. Conditions of concurrence of these points are investigated.