Упругий эквивалент

>

restart;

Процедура дифференцирования по t любого порядка

>	Dif:=proc(x,i) if i=0 then x else diff(x,t$i) fi end:

>	with(LinearAlgebra):

Задаем матрицу

>	B:=Matrix(2):

Деформация ползучести и напряжение

>	p:=P(t): s:=S(t):

Обозначения

>	x1:=p:   x2:=s:

>	with(PDEtools):

>	declare(P(t),S(t));

Определяющее соотношение

>	eq[1]:=diff(p,t)*p^alpha-A*s^n;

Определяющее соотношение, продифференцированное по времени

>	eq[2]:=Dif(eq[1],1):

Замена переменных

>	eq3:=subs(diff(p,t)=p1,subs(diff(p,t$2)=p2,{eq[1],eq[2]})):

Выражаем скорость и ускорение деформации ползучести из опред.соотн.

>	sol:=solve(eq3,{p1,p2}):assign(sol):

Процедура варьирования

>	AA:=proc(eq,i,j) local xx;

>	subs(xx=Dif(x||j,i),diff(subs(Dif(x||j,i)=xx,eq),xx));

>

end proc:

Матрица коэффициентов при вариациях

>	for i to 2 do

>	for k to 2 do

>	B[k,i]:=AA(eq[k],i-1,1)+G*AA(eq[k],i-1,2);

>

od:

>

od:

Условие нестабильности

>	det1:=Determinant(B):

Подставляем ранее найденные скорость и ускорение

>	usl:=subs(diff(S(t),t)=0,subs(diff(P(t),t)=p1,subs(diff(P(t),t$2)=p2,det1))):

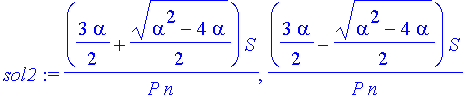
Находим упругий эквивалент

>	sol2:=solve(usl,G);

>	evalf(subs(S(t)=4,P(t)=0.2,{sol2}));