Программа  9 с.101                       Кирсанов М.Н, 

Графы в Maple

Транзитивное замыкание

>	restart: with(LinearAlgebra): n:=4:

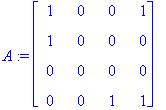
>	A:=Matrix([[1,0,0,1],[1,0,0,0],[0,0,0,0],[0,0,1,1]]);

>	`IsMatrixShape/trnztv` := proc(A)

>	local i,j,m,S:

>

S:=true:

>	for i to n do

>	for j to n do

>	for m to n do

>	if(A[i,m]*A[m,j]=1) then S:= S and is(A[i,j]=1);fi;

>

od;

>

od;

>

od:

>

end:

>	IsMatrixShape(A,trnztv);#Проверка транзитивности

>	if IsMatrixShape(A,symmetric) then print("Неограф") else print("Орграф"); fi;

>	if Trace(A)=n then print("Граф рефлексивного отношения");fi;

>	if Trace(A)=0 then print("Граф антирефлексивного отношения");fi;

>	if IsMatrixShape(A,zero) then print("Пустой граф"); fi;

>	A:=subs(1=true,0=false,A);

>	for m to n do #Алгоритм Уоршолла

>	for i to n do

>	for j to n do

>	A[i,j]:=A[i,j] or (A[i,m] and  A[m,j]);

>

od;

>

od;

>

od;

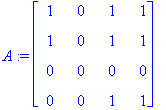
>	A:=subs(true=1,false=0,A);

>	IsMatrixShape(A,trnztv);#Проверка транзитивности