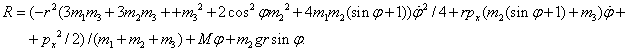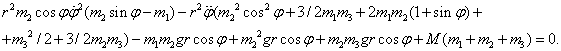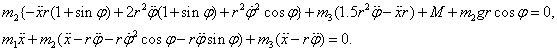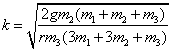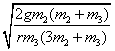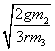|
АНАЛИЗ
ВЫРОЖДЕННОГО СЛУЧАЯ КОЛЕБАНИЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Кирсанов
М.Н., Федорова М.И.
Московский
Энергетический Институт (Технический Университет). Москва. Россия.
Рассмотрим
задачу о качении цилиндра радиуса r по бруску. Брусок скользит по
гладкой горизонтальной поверхности (рис.1). Качение происходит без
проскальзывания. Масса бруска равна 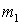 , масса точки,
расположенной на ободе цилиндра, равна , масса точки,
расположенной на ободе цилиндра, равна 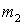 , цилиндра
— , цилиндра
— 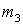 . К цилиндру приложен момент M. . К цилиндру приложен момент M.
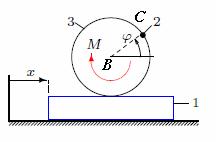
Рис.1
За обобщенные координаты
примем смещение бруска 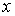 и угол поворота цилиндра и угол поворота цилиндра 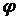 . Для начала, решим задачу кинематики.
Найдем выражения скорости точки с массой . Для начала, решим задачу кинематики.
Найдем выражения скорости точки с массой 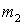 и
оси цилиндра B через выбранные обобщенные
скорости и
оси цилиндра B через выбранные обобщенные
скорости  и и 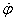 . Имеем . Имеем
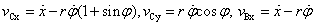 . Кинетическая энергия системы имеет
вид . Кинетическая энергия системы имеет
вид 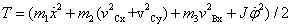 , где , где 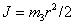 – момент
инерции однородного цилиндра. Потенциальная энергия равна – момент
инерции однородного цилиндра. Потенциальная энергия равна 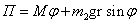 . Функция Лагранжа: . Функция Лагранжа:
 Обобщенная
координата Обобщенная
координата 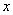 не входит в выражение для не входит в выражение для 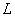 и является циклической. Найдем
обобщенный импульс и является циклической. Найдем
обобщенный импульс 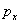 , соответствующий
циклической координате , соответствующий
циклической координате 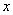 . Имеем циклический интеграл . Имеем циклический интеграл
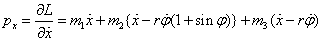
В силу уравнения Лагранжа, 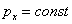 . Выразим отсюда циклическую скорость: . Выразим отсюда циклическую скорость:
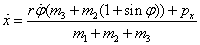 . .
Запишем функцию Рауса, 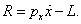 После подстановки сюда выражения для После подстановки сюда выражения для 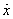 и некоторых преобразований получим и некоторых преобразований получим
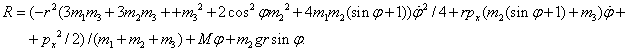
Функция Рауса
удовлетворяет уравнению
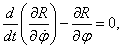
или
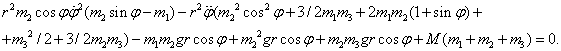 (1) (1)
Из этого уравнения
можно найти  . Циклическая
координата определяется из интеграла . Циклическая
координата определяется из интеграла
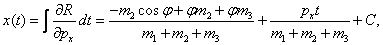
где C
— постоянная интегрирования. Константы 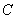 и и 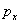 определяют
из начальных условий для определяют
из начальных условий для 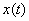 . Заметим, что уравнения
Лагранжа 2-го рода дают связанную систему уравнений: . Заметим, что уравнения
Лагранжа 2-го рода дают связанную систему уравнений:
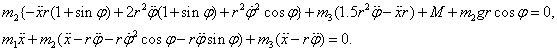
Решение системы находим с помощью
математического пакета Maple. Обнаружена
интересная особенность решения. С уменьшением массы 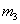 , решение ведет себя трудно предсказуемым образом. Наблюдается необъяснимый на первый взгляд скачкообразный рост угла , решение ведет себя трудно предсказуемым образом. Наблюдается необъяснимый на первый взгляд скачкообразный рост угла 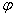 . Объяснение этого факта дает аналитическое решение. Найдем решение уравнения Рауса в рядах. Зададим начальный угол . Объяснение этого факта дает аналитическое решение. Найдем решение уравнения Рауса в рядах. Зададим начальный угол 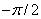 .
Получим решение .
Получим решение
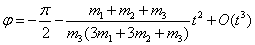 . .
Масса
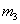 содержится в
знаменателе, что и объясняет замеченный эффект. Увеличение числа членов ряда не
меняет этой особенности. Рассматривая малые собственные колебания системы около
положения содержится в
знаменателе, что и объясняет замеченный эффект. Увеличение числа членов ряда не
меняет этой особенности. Рассматривая малые собственные колебания системы около
положения 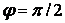 и линеаризируя (1), получим частоту
собственных колебаний системы и линеаризируя (1), получим частоту
собственных колебаний системы 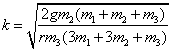 . С увеличением
массы бруска частота колебаний падает с . С увеличением
массы бруска частота колебаний падает с 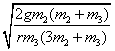 до до
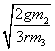 . .
Работа выполнена при поддержке Российского
фонда фундаментальных исследований (проекты 09-01-00756-а, 09-08-01184-а).
|