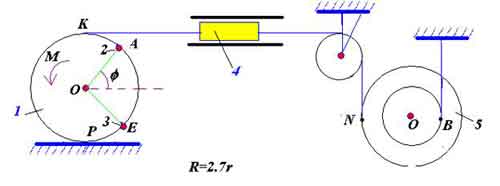
Дано

m₁=5кг, m₂=2кг, m₃=5кг, m₄=2кг, m₅=4кг

 R₁=0.63м, R₅=0.33м, M=26Нм

 r₅= R₅/2.3;

Найдем кинетическую энергию

 T=T1+T2+T3+T4+T5

             1 

Из графа P------àO получим Vox=- ω R₁, где ω =dφ/dt

           π/2  

             1 

Из графа 0------àA получим

             φ

Vax= Vox - ω R₁sinφ= - ω R₁ (1+sinφ),

Vay=Voy+ ω R₁cosφ = ωR1cosφ,

Аналогично, из графа

             1 

         0------àA получим

             φ-п/2

Vex= Vox- ωR1sin(φ-п/2)= - ω R₁(1-cosφ),

Vey=Voy+ ωR1cos(φ-п/2) = ω R₁sinφ,

Так как в точке P находится МЦС колеса 1, то, очевидно,

Vkx= 2Vox, или, из графа

             1 

        P------àK получим Vkx=Vpx- ωsin(п/2)2R1=- 2ω R₁.

           π/2  

Нить нерастяжимая, следовательно, V4x=Vkx, а Vny=-Vkx (минус, т.к. если точка К движется влево, то N поднимается, или наоборот, и проекции имеют разные знаки).

Для нахождения скорости и угл.скорости тела 5 составим граф

            5 

        N------àB и получим Vby=VNy+ ω₅cos(0)( R₅+ r₅);

            0  

Vby=0, отсюда найдем угл.скорость

        ω₅=-VNy/(R₅+ r₅)=Vkx/( R₅+ r₅)=- 2ω R₁/( R₅+ r₅).      

Из графа к центру

            5

        B------à0  получим

            п

Vоy=Vby+ ω₅cos(п) r₅

Vby=0, отсюда найдем угл.скорость

          Vоy=-ω₅r5=2ωr5/( R₅+ r₅) R₁

1. Кинетическая эн. точки А: T2=Ta=Va²ma/2=maω²R₁²(1+sinφ)

2. Кинетическая эн. точки E: T3=Te=Ve²me/2=meω² R₁²(1-cosφ)

3. Кинетическая эн. тела  4: T4=Vk²m4/2=2m4ω² R₁²

4. Кинетическая эн. тела 5 (плоское движение):

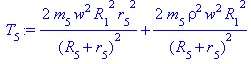
Где радиус инерции по условию

Окончательно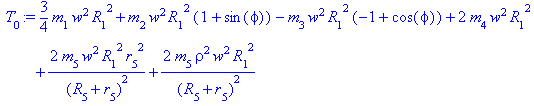

Обобщенная сила:

 Q=(- m₂*g*Vay-m3*g*Vey+M*w-m5*g*Voy)/w

или

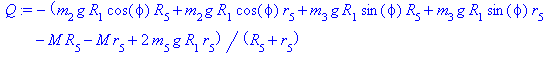
Уравнение Лагранжа 2-го рода

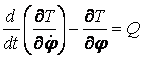
где

=

_(*)

=

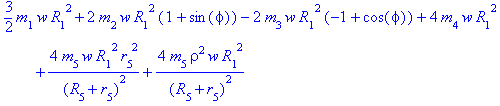Подставляем численные значения, дифференцируем (*) по времени,

В итоге имеем дифференциальное уравнение

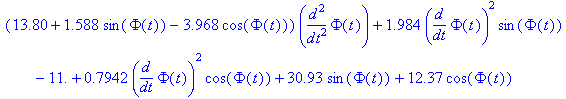
По условию   =0. Найдем искомое ускорение

 ε=-27.46/11.12=-2.267рад/с²