Уравнение Лагранжа 2-го рода
Приведем краткие решения некоторых задач.
В решении задач на составление уравнения Лагранжа 2-го рода наибольшая трудность
состоит в нахождении кинетической энергии и обобщенной силы. Здесь даны
именно эти вычисления. Дифференцирование же кинетической энергии по
обобщенной координате в основном одинаково для всех задач.
Например, если кинетическая энергия имеет вид
то частные производные легко вычисляются:
Полная производная по времени
Окончательно уравнение примет вид
Аналогичные задачи см. Кирсанов М.Н. Решебник. Теоретическая механика/Под ред. А. И. Кириллова.- М.:ФИЗМАТЛИТ, 2002.- 384 c. (с. 300.) . Информацию об этой книге и Maple-программы для решения задач можно найти на сайте WWW.AcademiaXXi.ruWWW.AcademiaXXi.ru, заказ книги -- WWW.FizmatKniga.ruWWW.FizmatKniga.ru
.
Задача 1
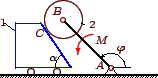
Решение
Составляем кинематический граф
где С - точка касания диска и груза. Соответствующие уравнения для проекций скоростей
Учитывая, что
и 
, получим угловую скорость диска и скорость
груза
Вычислим кинетическую энергию груза, совершающего поступательное движение
Из графа
сразу же следует
и
.
Кинетическая энергия плоского движения диска
Суммарная кинетическая энергия имеет вид
Обобщенная сила
Задача 2
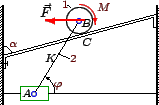
Решение
Составляем кинематический граф
Соответствующие уравнения для проекций скоростей
Учитывая, что
, получим
Для вычисления обобщенной силы потребуется угловая скорость цилиндра. Найдем ее из графа
где С - точка касания диска. Получим
или
откуда
Определим скорость центра масс стержня, составим кинематический граф
Вычислим кинетическую энергию однородного цилиндра, катящегося по неподвижной поверхности,
Вычислим кинетическую энергию стержня, совершающего плоское движение
Суммарная кинетическая энергия имеет вид
Обобщенная сила
