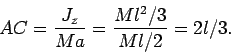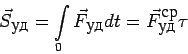Определения

(1)

отличается от импульса неударных сил тем, что время удара мало, ударные силы велики, а принимает конечное значение. Поэтому изучая удар будем пренебрегать

• неударными силами по сравнению с ударными,
• перемещениями точек тела во время удара.

Теорема об изменении количества движения в случае удара имеет вид

(2)

Интегрируя теорему об изменении момента (относительно точки ) количества движения

(3)

Центр удара

Твердое тело массой вращается на оси, закрепленной на в подшипниках и . Подшипник имеет подпятник, создающий реакцию, направленную вдоль оси. Определим, чему равны импульсивные реакции и при ударе. Выберем оси координат так, что центр масс тела находился в плоскости . При ударе возникнет пять импульсивных реакций: три в опоре и две в опоре (рис. 1).

Обозначим: -- расстояние центра масс от оси, -- расстояние между подшипниками, -- угловая скорость тела до удара, -- угловая скорость после удара.

                     

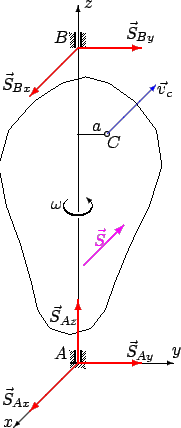
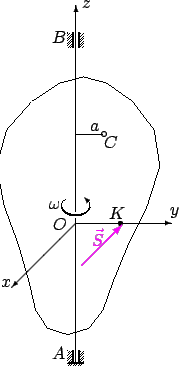
 Рис. 1                                                           Рис. 2
Запишем уравнения (2), (3) в проекциях на оси координат. Так как проекции кинетического момента имеют вид , , , то получим

			(4)
			(5)
			(6)
			(7)
			(8)
			(9)

Составление правых частей (4- 9) аналогично составлению уравнений равновесия пространственной статики, только вместо сил здесь берутся их импульсы. В системе (4-9) шесть неизвестных: ударные реакции , , , , и разность угловых скоростей .

Найдем условия, при которых не возникают импульсные (ударные) реакции шарниров. Известно, что в механических устройствах ударные реакции способствуют износу и могут привести к разрушению.

Положим в (4-9): , . Из (5) и (6) сразу же получим, что вектор внешнего ударного импульса должен лежать в плоскости, параллельной : , . Заметим, что при , вид системы (4-9) не зависит от выбора начала координат. Перенесем начало координат по оси так, чтобы импульс лежал в плоскости (рис. 2). Так как , , то из (7) и (8) следует, что центробежные моменты инерции тела относительно новых осей равны нулю: , . Это возможно для тел, обладающих плоскостью симметрии . Из (4) при следует

где обозначено . Из последних двух уравнений сразу же получим

(10)

Пример. Однородный стержень длиной шарнирно закреплен на одном конце. Вычислим, на каком расстоянии к стержню надо приложить ударный импульс, так чтобы удар не передался оси вращения . Найдем центр удара. Момент инерции стержня относительно точки (или оси , проходящей через ): . Центр масс находится на расстоянии от оси вращения. Отсюда, согласно (10) получим