Определение особых точек. Вариация и дифференцирование                                       

>

restart;

Процедура дифференцирования по t любого порядка

>	Dif:=proc(x,i) if i=0 then x else diff(x,t$i) fi end:

>	with(LinearAlgebra):

>	with(PDEtools,declare):declare(x(t));

Максимальный порядок

>	N:=1: c:=1:b:=14:a:=5:Порядок:={0,3};x1:=4: A:=Matrix(N+1):

Уравнение

>	eq:=diff(x(t),t$2)*b*x(t)+a*diff(x(t),t)^2+c*x(t)^2;   D(a):=0:D(b):=0:D(c):=0:

Вариация

>	z[1]:=D(eq):

Вариация производных уравнения по времени порядка от 1 до N

>	for k to N do z[k+1]:=D(diff(eq,t$k)):od:

Порядок искомых производных (для уравнения 2 порядка)

>	SET:={seq(j,j=0..N+2)} minus Порядок:

Заполнение матрицы

>	for i to N+1 do

>	for j to N+1 do

>	A[i,j]:=coeff(z[i],D(Dif(x(t),SET[j]))):

>

od:

>

od:

>

A;

>	Dtr:=Determinant(A);

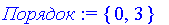
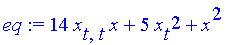
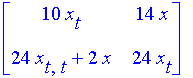
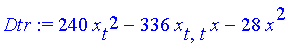
Подставляем даные и находим   х

>	evalf(solve(subs(diff(x(t),t)=x1,Dtr),x(t)));
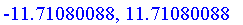
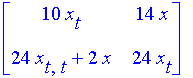