С.А.Бернштейн. Очерки по истории строительной механики. М.1957

ПОИСКИ УДОБНОГО МЕТОДА ВЫЧИСЛЕНИЯ ПЕРЕМЕЩЕНИИ

И Берто, и Клапейрон дали выражение уравнения трех моментов только для одного частного случая — сплошной равномерной нагрузки на балке. Для дальнейшего обобщения необходимо было научиться вычислять углы поворота на опорах простой балки от произвольной нагрузки, так как именно эти углы входят в правые части уравнений.

Классический аналитический метод был крайне неудобен для решения этой задачи. Действительно, он давал гораздо больше, чем для нее было нужно, — уравнение всей линии прогиба, из которой требуется определить только углы поворота по концам, — и за эту избыточную полноту решения приходилось расплачиваться чрезмерной трудоемкостью вычислений, от которой лишь частично избавлял метод интегрирования Клебша. Необходимо было найти прямой метод вычисления, позволяющий сразу получить нужные перемещения, - в данном случае углы поворота.

Максвелл
Максвелл

От нахождения такого прямого метода зависела возможность практического расчета любой статически неопределимой системы, работающей на изгиб. В настоящее время мы применяем для этого формулу Мора — Максвелла в аналитической или графоаналитической форме.

Мор
О.Мор

Для балок столь же простое решение дает графоаналитический метод Мора. Но было бы ошибкой думать, что оба эти приема родились внезапно и не имели предшественников. В действительности, такие предшественники были, хотя они забыты и, если можно так выразиться, "забиты" формулой Мора. Мы считаем уместным, хотя бы отчасти, воскресить забытую историю поисков удобного метода вычисления перемещений, которые завершились в работах Мора. Первый шаг сделал в 1854 г. Бресс [22], и мы уже приводили в очерке втором выведенные им формулы для вычисления перемещений криволинейного стержня. Применительно к прямому стержню (балке) эти формулы дают выражение прогиба и угла поворота в виде


y=xj0- у
х 		x

0 
 xM
EJ
 dx
где j0 — угол поворота на левой опоре, с которой совпадает начало координат. Несомненно, эти формулы представляют очень значительный прогресс по сравнению с аналитическим методом двукратного интегрирования, так как они дают возможность прямого вычисления прогиба и угла поворота в любом сечении балки, не требуют определения произвольных постоянных и заменяют двукратное интегрирование однократным. По существу в этих формулах полностью заключен будущий графоаналитический способ Мора, так как первая из них, очевидно, выражает момент от фиктивной нагрузки [M/EJ], а вторая — поперечную силу от той же нагрузки. Но хотя Бресс был первым ученым, которому пришла в голову счастливая мысль изображать закон изменения изгибающего момента в виде графика (эпюры), но он не сумел дать графостатическое истолкование своих формул. Сейчас нам даже странно представить себе, что для этого потребовалось еще 14 лет: графоаналитический метод Мора был опубликован в 1868г.

Идея использования эпюры моментов как инструмента для вычисления прогиба, т. е. идея графоаналитического метода, возникла однако за 13 лет до Мора: впервые ее применил русский инженер Беспалов [20] в 1855 г. Это имя давно забыто и ни разу не встречалось нам ни в одной книге по строительной механике. Маленькая книжечка Беспалова, изданная в год Крымской войны, содержит элементарное изложение основных задач сопротивления материалов, полностью стоящее на уровне своего времени, но не представляющее ничего оригинального, кроме нескольких страниц (стр. 26—30), где изложен совершенно необычный прием вычисления прогиба консоли, основанный на методе приравнивания работы внешних и внутренних сил (как известно, этот метод был предложен Клапейроном). Для вычисления работы внутренних сил еse (Множитель 1/2 у Беспалова пропущен). Беспалов строит две эпюры: эпюру напряжения и эпюру удлинения для произвольного волокна по длине консоли (рис. 55), а затем сочетает их в одну эпюру, откладывая по оси абцисс удлинения, а по оси ординат напряжения. Беспалов без труда доказывает, что контур этого нового графика очерчен по дуге параболы, а потому его площадь, выражающая работу, равна 2/3smaxеe. Отсюда он получает правильное выражение прогиба консоли.

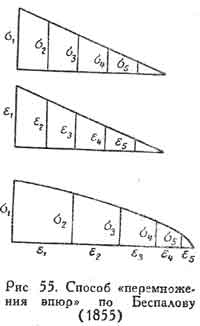
Способ перемножения эпюр по Беспалову

В этом приеме можно, пожалуй, увидеть зародыш будущего метода "перемножения эпюр", данного впоследствии Мюллером-Бреслау на основе фомулы Мора. Беспалов первым догадался использовать эпюры, т. е. графики внутренних усилий, для графоаналитического вычисления прогиба. И хотя примененный им для этого прием может показаться сейчас несовершенным, но не надо забывать, что эта мысль никому не приходила в голову ранее Беспалова, и что после него прошли три десятилетия, прежде чем она была применена в общем виде Мюллером-Бреслау (1884).

Через 3 года после Беспалова (работа которого, по-видимому, осталась незамеченной и в иностранной, и даже в русской науке) мы встречаем в курсе прикладной механики Магистра [157] новую идею. Для того же случая консоли с грузом на конце Магистр получает формулу прогиба в виде

y= P
EJ
 у
х 		x2dx,
используя уравнения Бресса, и вычисляет этот интеграл, как статический момент фиктивных сил xdx. Магистр ссылается при этом на Понселе, но без указания на источник, которого нам разыскать не удалось. Кому бы ни принадлежала эта идея Магистру или Понселе,—она очень интересна, так как представляет еще один подход к графоаналитическому методу. Но в противоположность Беспалову, который исходит из эпюры, Магистр не замечает, что треугольный график фиктивной нагрузки x, от которой он берет статический момент, представляет собой эпюру моментов. Таким образом, идеи Беспалова и Магистра (или Понселе) как бы взаимно дополняют друг друга; казалось бы достаточно было бы положить перед собой на стол эти две книжки, раскрыв первую на странице 26, а вторую — на странице 537, чтобы додуматься до графоаналитического метода. Но Мор додумался до него только через 10 лет. В истории строительной механики мы уже не раз отмечали случаи, когда тот или иной ученый стоит перед готовым созревшим открытием и не видит его. История поисков метода вычисления перемещений особенно богата примерами такой близорукости. Бресс дал готовые формулы графоаналитического метода; Магистр показал их графостатический смысл, а Беспалов дал пример использования эпюр для вычисления прогиба. Предложение Магистра сразу переводило задачу вычисления прогиба в область графической статики, где применение веревочного многоугольника для вычисления статических моментов уже было к этому времени известно. И тем не менее, когда Кульман выпустил в 1866 г. свою известную книгу по графической статике [99], в которой он придал графическим методам небывалую до этого общность и стройность, он не только не перевел приема Магистра на графический язык, но безапелляционно заявил, что задача вычисления прогибов балки навсегда останется недоступной для применения графических методов, так как эти прогибы ничтожно малы по сравнению с длиной балки. Открытый Мором двумя годами позже графический метод построения линии прогиба с помощью веревочного многоугольника дал хороший урок Кульману. Но, помимо оплошного утверждения Кульмана, самая его мотивировка вызывает крайнее удивление: неужели Кульман не знал, что продольный профиль проектируемой железнодорожной линии вычерчивается инженерами в разных масштабах по вертикальной и горизонтальной оси, и что их, таким образом, ничуть не смущает ничтожная разница вертикальных отметок по сравнению с длиной линии?

Способ перемножения эпюр по Мюллеру-Бреслау

После появления работы Мора 1868 г. [158], содержавшей графический метод построения линии прогиба (который вскоре же был превращен в графоаналитический), дальнейшие открытия следуют одно за другим. В 1874 г. Мор дает обобщение формулы Максвелла, известное под названием формулы Мора—Максвелла [138], а в 1875г. Кастилиано [159] публикует свою теорему. Все эти методы вычисления перемещений мы считаем достаточно известными читателю, и потому на них не останавливаемся. Таким образом, задача нахождения удобного метода вычисления перемещений была решена к началу 70-х годов.

Надо подчеркнуть, что вычисление перемещений путем непосредственного интегрирования формулы Мора, несмотря на математическую простоту, все же не удовлетворило инженеров и применялось неохотно, пока не был найден способ освободиться от этого интегрирования. 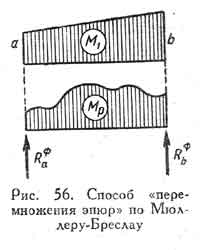Первый такой способ дал Мюллер-Бреслау; он основан на условии линейности уравнения момента от единичной силы и использует графическое представление моментов в виде эпюр. Если M1 — эпюра моментов от единичной силы, линейная на рассматриваемом участке, а Mp — эпюра моментов от нагрузки (рис. 56), то по Мюллеру-Бреслау интеграл Мора

у
х 		M1Mpdx
(жесткость EJ опускаем) равен сумме произведений фиктивных реакций от эпюры Mp на крание ординаты эпюры M1:
у
х 		M1Mpdx=aRaF+bRbF
Но и этот несомненно простой способ не нашел широкого распространения, и формуле Мора в течение нескольких десятилетий пришлось выдерживать трудную борьбу с ее конкурентам — теоремой Кастильяно. Окончательную победу формула Мора смогла одержать только с помощью способа вычисления, данного молодым советским инженером Верещагиным [161]. Этот способ хорошо известен: он сводит вычисление интеграла Мора к умножению площади эпюры Mp на ординату линейной эпюры M1, находящуюся против центра тяжести этой площади. Нетрудно установить переход от приема Мюллера-Бреслау к приему Верещагина; но интересно, что только последний получил сразу широчайшую популярность и содействовал быстрому освоению метода Мора в кругах инженеров-строителей1. Для балок вычисление перемещений графоаналитическим способом Мора получило в России широкое распространение немедленно после его опубликования, приняв несколько своеобразную трактовку "шести строк" (нагрузка, поперечная сила, изгибающий момент, кривизна, угол, поворота и прогиб), которая способствовала глубокому пониманию существа этого метода и достаточно хорошо известна читателям. Именно это понимание существа было причиной того недоумения, с которым было встречено в наших научных кругах наивное "открытие" американской науки 1930-х годов [162], предлагавшее принимать за фиктивную нагрузку не эпюру моментов, а эпюру поперечной силы, причем из восторженного тона американских журналов можно было заключить, что обычный графоаналитический метод Мора за океаном к тому времени еще не был известен.

Footnotes:

1Возможно, что этому способствовала самая форма способа Верещагина, напоминавшая хорошо знакомый прием загружения линий влияния.


File translated from TEX by TTH, version 3.64.
On 15 Dec 2006, 20:06.