Кусково
Вопросы к экзамену по высшей математике
(АиУ-6, Уи-7, Уик-8. 14 июня 2004)

    Интегралы
  1. Комплексные числа. Определение. Основные действия.
  2. Извлечение корня из комплексного числа и возведение в степень.
  3. Комплексные числа. Формула Эйлера.
  4. Первообразная. Неопределенный интеграл. Определение.
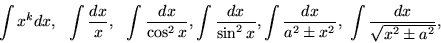
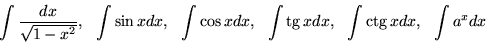
  5. Таблица интегралов.
    Таблица интегралов
    Таблица интегралов
  6. Свойства неопределенных интегралов.
  7. Способы интегрирования. Замена переменных. Способы интегрирования функций, содержащих квадратный трехчлен.
  8. Интегрирование по частям.
  9. Правильные и неправильные рациональные дроби. Интегралы от рациональных дробей.
  10. Интегралы от иррациональных функций.
  11. Три подстановки Эйлера.
  12. Интегрирование дифференциального бинома.
  13. Интегралы от тригонометрических функций. Универсальная подстановка.
  14. Функции, интегралы от которых не выражаются через элементарные функции. Эллиптический интеграл. Интегральный синус, косинус, логарифм.
  15. Определенный интеграл. Существование. Нижняя и верхняя интегральные суммы. Равномерная непрерывность функции.
  16. Шесть свойств определенного интеграла, включая теорему о среднем.
  17. Формула Ньютона-Лейбница.
  18. Несобственные интегралы. Сходимость и абсолютная сходимость. Интеграл от разрывной функции.
  19. Дифференцирование интеграла, зависящего от параметра.
  20. Приложение определенного интеграла. Площадь плоской фигуры в декартовой и полярной системе координат.
  21. Длина дуги кривой, заданной параметрически.
  22. Длина дуги. Длина дуги в полярных координатах.
  23. Вычисление объем тела по параллельным сечениям.
  24. Вычисление объем тела вращения.
  25. Поверхность тела вращения.
  26. Центр тяжести и моменты инерции. Примеры (круг, дуга окружности).
  27. Двойной интеграл. Свойства. Правильная область. Вычисление с помощью двукратного интеграла.
  28. Изменение пределов интегрирования в двойном интеграле. Вычисление объема.
  29. Двойной интеграл в полярной системе координат. Функциональный определитель Якоби. Пример применения.
  30. Вычисление площади поверхности и моментов инерции с помощью двойного интеграла.
  31. Эллипс инерции. Неравенство Буняковского.
  32. Тройной интеграл и его вычисление.
  33. Криволинейный интеграл. Свойства.
  34. Формула Грина.
  35. Условие независимости криволинейного интеграла от пути интегрирования.
  36. Поверхностный интеграл. Формула Стокса.
  37. .
  38. Элементы теории поля. Определение поля. Потенциал. Ротор. Условие потенциальности. Связь с оператором Гамильтона.
  39. Элементы теории поля. Дивергенция. Градиент. Оператор Лапласа. Гармонические функции. Связь с оператором Гамильтона.

    40. Ряды
  40. Ряды. Частичные суммы. Отбрасывание нескольких членов ряда.
  41. Необходимый признак сходимости ряда.
  42. Достаточный признак расходимости ряда.
  43. Теоремы сравнения. Доказательство расходимости гармонического ряда.
  44. Признак Даламбера. Пример.
  45. Признак Коши. Пример.
  46. Интегральный признак. Пример.
  47. Знакочередующиеся ряды. Теорема Лейбница. Абсолютная сходимость. Условная сходимость.
  48. Функциональные ряды. Область сходимости.
  49. Степенные ряды. Радиус сходимости.

    50. Дискретная математика
  50. Множества, собственное подмножество. Объединение множеств, пересечение, разность, симметрическая разность, абсолютное дополнением. Универсальное множество. Свойства операций (коммутативность, ассоциативность, дистрибутивность, идемпотентность).
  51. Свойства универсального и пустого множеств. Закон двойного дополнения.Законы де Моргана. Парадокс Рассела. Булеан. Мощность множества. Мощность булеана.
  52. Прямое произведение. Упорядоченная пара. Три свойства прямого произведения. Соответствие между множествами. Область определения соответствия. Первая проекция соответствия. Область значений соответствия. Вторая проекция. Сечение соответствия.
  53. Обратное соответствие. Пустое соответствие. Полное соответствие. Булевы матрицы. Дизъюнкция и конъюнкция. Композиция соответствий. Условие существования композиции.
  54. Отображение. Отображение функциональное. Шесть свойств отображений. Сюръективное, инъективное, биективное отображение.
  55. Композиция отображений. Ассоциативность композиции отображений. Обратное отображение. Единичное отображение. Левое и правое обратное отображение.
  56. Лемма о единичной композиции двух отображений.
  57. Теорема о существовании обратного отображения.
  58. Отношения унарные и бинарные. Граф отношения.Матрица отношения. Единичное отношение. Полное отношение. Обратное отношение. Свойства отношений (рефлексивность, антирефлексивность, симметричность, антисимметричность, асимметричность, транзитивность).
  59. Композиция бинарных отношений. Условие транзитивности.
  60. Замыкание отношения. Рефлексивное замыкание. Транзитивное замыкание. Теорема о виде транзитивного замыкания. Вид транзитивного рефлексивного замыкания.
  61. Два алгоритма нахождения транзитивного замыкания. Отношение эквивалентности. Класс эквивалентности. Фактор-множество. Разбиение.
  62. Отношение порядка. Предпорядок. Полный порядок. Частичный порядок. Строгий порядок. Диаграмма Хассе. Отношение Парето. Алфавит. Лексикографический порядок.

    63. Графы
  63. Граф, ребро, вершина, дуги, ориентированные и неориентированные графы. Кратные ребра, мультиграф, петли. Конечный граф. Пустой граф. Полный граф. Граф двудольный. Полный двудольный граф.
  64. Матрица инцидентности. Список ребер. Матрица смежности. Матрица Кирхгофа.
  65. Лемма о рукопожатиях. Изоморфные графы. Граф регулярный (однородный).
  66. Маршрут. Эксцентриситет вершины. Радиус, диаметр, центр, периферия графа. Взвешенный граф. Матрица весов.
  67. Маршрут циклический. Цепь. Путь. Контур. Простая цепь. Цикл. Простой цикл.

МГТУ МАМИ