ОЛИМПИАДА ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ

МАДИ(ГТУ)-2006

Задача  1 (5 баллов)

Плита,  имеющая вес  G= 10  [кН],  покоится  на  двух  цилиндрах  и занимает  положение  под углом  j=p/3   к горизонту. Все связи  с цилиндрами  осуществляются без проскальзывания. Плита удерживается в покое пружиной  с  жесткостью   c=20  [кН/см],  и  с  направлением  оси,  указанном  на рисунке.  Определить деформацию  пружины  D [см].

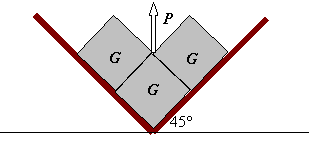
Задача  2 (5 баллов)

 На двух  наклонных  к горизонту под  углом  45°   плоскостях  лежат  три  куба, каждый  весом  G=5 [кН].    Задан  коэффициент  трения   скольжения     между  соприкасающи-мися  плоскостями  f=1/5.  Какой   вертикальной  силой   Р , приложенной  к  нижнему  кубу,  можно его   поднять?  

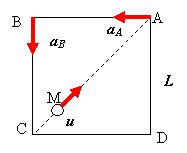
Задача  3 (5 баллов)

В каком   положении   величина   скорости  точки  движущейся  по параболе  y²=4x  в два  раза   больше,  чем скорость  её  проекции   по  оси  x?  (Определить  координаты  (x,y)  для  этого  положения  точки.)

Задача  4 (5 баллов)

Квадрат  ABCD  со стороной  L=1 м  перемещается  в  плоскости  таким  образом, что  ускорения  точек A и B  имеют  направления, показанные  на  рисунке, а  величины  ускорений a_A= a_B= 1 м/с². Вращательная часть движения квадрата – ускоренная. По диагонали  квадрата  движется  точка  М  с  постоянной  по величине  относительной  скоростью  u=1 м/с. Найти ускорение  точки  М (численную величину и направление), когда  она  находится в  середине  квадрата. Полученные результаты обосновать.