Правило Верещагина

Рассмотрим интеграл, от произведения эпюр моментов, возникающий в формуле Мора, у х b a  f(x)(kx+m)dx, где y=f(x) нелинейная эпюра моментов (обычно от действия распределенной нагрузки), а y=kx+m - линейная. Выведем простое правило вычисления этого интеграла. Раскроем скобки и преобразуем у х b a  f(x)(kx+m)dx = k у х b a  f(x)xdx + m у х b a  f(x)dx. Второй интеграл это просто площадь нелинейной эпюры у х b a  f(x)dx = W, а первый - статический момент у х b a  xf(x)dx = S площади нелинейной фигуры относительно оси y. Так как координата центра тяжести имеет вид xc = S/W, получим у х b a  f(x)(kx+m)dx = kxcW+ mW = W(kxc+m) = Wh. 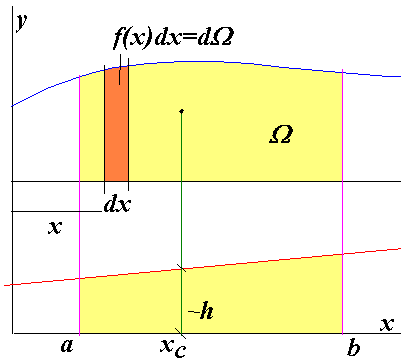Правило Верещагина можно сформулировать так - интеграл от произведения нелинейной эпюры и линейной равен произведению площади нелинейной и ординаты линейной, вычисленной под центром тяжести нелинейной. На рисунке - синяя кривая это нелинейная эпюра, красная прямая - линейная. Интегрирование ведется на участке ab.