Ряд гармонический

Николай Владимирович Андреевский

Н.В.Андреевский
Ряд гармонический и другие

1  

Гармоническим рядом называют сумму бесконечного количества членов обратных последовательным числам натурального ряда. Его обозначают
H = 1 + 1
2
 + 1
3
 + 1
4
 + ...
Гармонический ряд является исторически первым примером численного ряда, члены которого неограниченно убывают и который, несмотря на это, расходится, т.е. для которого

lim
n®Ґ 
 Hn = Ґ.
Расходимость его была доказана Лейбницем в 1678 г. Название ряда объясняется тем, что каждые три последовательных его члена, начиная со второго, un-1, un, un+1, удовлетворяют одному и тому же правилу: средний член связан с крайними равенством
un = 2un-1un+1
un-1 + un+1
 .
Подобная зависимость чисел называют гармоническим делением или золотым сечением.
В курсе математического анализа гармонический ряд является основным и играет не менее значительную роль, чем убывающая геометрическая последовательность.

2  

Докажем расходимость гармонического ряда.
Если

lim
n®Ґ 
 ж
и 		1+ 1
n
 ц
ш 		n

 
 = e,
где подпредельная функция монотонно возрастает, то
ж
и 		1+ 1
n
 ц
ш 		n

 
 < e,
где e=2.718.... Возьмем от обеих частей неравенства натуральный логарифм:
nln ж
и 		1+ 1
n
 ц
ш 		< 1,
или
1
n
 > ln(n + 1) - ln(n).
При n = 1,2,3, ... n последовательно получим
1 > ln2 - ln1,

1
2
 > ln3 - ln2,

1
3
 > ln4 - ln3,
....
После сложения членов левой части неравенств получим
1 + 1
2
 + 1
3
 + 1
4
 + ... + 1
n
 > ln(n+1),
или
Hn > ln(n+1).
Если количество членов ряда неограниченно растет, то неравенство показывает, что сумма гармонического ряда неограниченно растет, т.е.

lim
n®Ґ 
 Hn = H =
lim
n®Ґ 
 ж
и 		1 + 1
2
 + 1
3
 + 1
4
 + ... ц
ш 		=Ґ.

3  

Из предыдущего видно, что гармонический ряд есть ряд расходящийся, т.е. сумма первых n его членов неограниченно растет с ростом количества взятых членов. Однако в отличие от других расходящихся рядов скорость роста суммы с увеличением числа членов замедляется. Гармонический ряд называют слабо расходящимся по сравнению с ростом n.
Докажем следующую теорему, характеризующую гармонический ряд в этом отношении.
Гармонический ряд
Теорема. При любом n имеет место приближенное равенство
1 + 1
2
 + 1
3
 + 1
4
 + ... + 1
n-1
 » ln(n)+ gn,
где 0 < gn < 1.
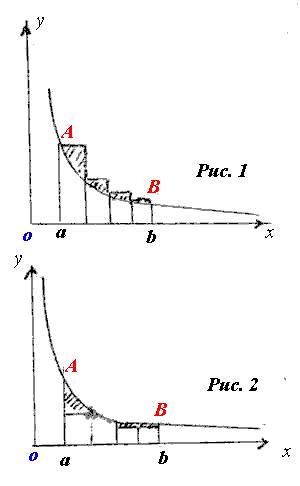
Доказательство. Пусть дана площадь криволинейной трапеции aABb, ограниченной равнобочной гиперболой, отнесенной к асимптотам, уравнение которой y = 1/x двумя ее ординатами aA и bB, уравнения которых x = 1 и x = n, и осью абсцисс. Пользуясь "формулами прямоугольников", вычислим эту площадь с недостатком (рис.2) и с избытком (рис.1). Разделив основание на n равных частей, найдем, что площадь aABb равна
у
х 		n

1 
 dx
x
 = ln(n).
Если взять левые ординаты (соответствующие точкам делений 1, 2, 3, ... n-1) за высоты прямоугольников, то получим площадь ступенчатой линии, превышающую площадь криволинейной трапеции. Отсюда вытекает неравенство
1 + 1
2
 + 1
3
 + 1
4
 + ... + 1
n-1
 > ln(n)
или
gn= ж
и 		1 + 1
2
 + 1
3
 + 1
4
 + ... + 1
n-1
 ц
ш 		- ln(n) > 0.
Если взять правые ординаты (соответствующие точкам делений 2, 3, ... n) за высоты прямоугольников, то получим площадь ступенчатой линии, меньшую площади криволинейной трапеции aABb (рис. 2). Поэтом можно сказать, что
1
2
 + 1
3
 + 1
4
 + ... + 1
n
 < ln(n).
Добавим к обеим частям неравенства 1- 1/n
1+ 1
2
 + 1
3
 + 1
4
 + ... + 1
n-1
 < ln(n) + 1 - 1
n
 .
или
gn= ж
и 		1 + 1
2
 + 1
3
 + 1
4
 + ... + 1
n-1
 ц
ш 		- ln(n) < 1- 1
n
Таким образом сумму первых n-1 членов гармонического ряда можно приближенно выразить через ln(n) следующим равенством
1 + 1
2
 + 1
3
 + 1
4
 + ... + 1
n-1
 » ln(n)+ gn.
С ростом количества членов гармонического ряда величина gn возрастает. Но 0 < gn < 1-1/n. Поэтому существует предел gn, меньший или равный единицы, т.е.

lim
n® Ґ 
 gn = C Ј 1.
Этот предел называют "эйлеровой постоянною". При помощи подсчетов Hn-1 и ln(n) удалось найти значение этого числа с большой точностью и получить C = 0.57721566490...

Рукопись Н. Андреевского

Андреевский Н.В.
Андреевский Николай Владимирович

Андриевский Владимир, отец Николая Владимировича

Андриевский Владимир, отец Николая Владимировича



Чарушникова А.

Письмо Н.В.Андреевскому
Владимир и Юля Андриевские. Вятка, 22 мая 1884 г.
Андреевский Н.В. Методы, формы и содержание работы математических кружков по элементарной математике и началам высшей. М. 1954. Автореферат