


Архив МЭИ



|
 по теор.механике 20 июня 2005
по теор.механике 20 июня 2005
 по дискретной математике. Основные тезисы
по дискретной математике. Основные тезисы


| 
| 
|
 экзаменационных задач по динамике
экзаменационных задач по динамике
|
Лекции по теоретической механике-2005 МЭИ(ТУ) Среда,13.35, ауд.H202 ЭЛ-1,3,5,6,8,11.
Результаты социологического опроса. Теория удара,HTML |
 Кинетическая энергия
Кинетическая энергия
| Результаты проверки посещаемости: на лекции 30 марта (сложное движение точки, сферическое движение) в 1 группе отсутствовали 2 студента, в 6 группе - 13 студентов. Всем этим студентам рекомендуем прочитать учебник Тарга С.М. (параграфы 64-67, 60, 61), все законспектировать и сдать конспект лектору. Если на контрольные вопросы студент даст правильные ответы, то его фамилия будет вычеркнута из ЧЕРНОГО списка. |
| Результаты проверки посещаемости: на лекции 4 мая (Решение задач с 2 степенями свободы (общее уравнение динамики, уравнение Лагранжа 2-го рода) в 8 группе отсутствовали 10 студентов. Всем этим студентам рекомендуем разобрать с. 294-296 из Решебника, все законспектировать и сдать конспект лектору. Если на контрольные вопросы студент даст правильные ответы, то его фамилия будет вычеркнута из ЧЕРНОГО списка. |
| Задания для Эл-01(03,05,06,08,11)-04 (PDF). 2005 | |||||
|---|---|---|---|---|---|
|
| ||||
|
|
|
| ||||
|
|
 ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
/Под ред. А.И.Кириллова - М.:ФИЗМАТЛИТ, 2002.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
/Под ред. А.И.Кириллова - М.:ФИЗМАТЛИТ, 2002.
|
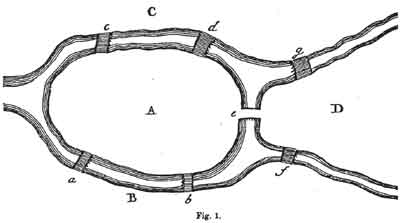
Л. Эйлер (1736): "... Эта задача, как мне сказали, довольно хорошо известна и связана вот с чем. В городе Кенигсберге, в Пруссии, есть остров, называемый Кнайпхов; река, окружающая его, делится на два рукава, что можно увидеть на рисунке. Рукава этой реки пересекает семь мостов a, b, c,d, e, f и g. В связи с этими мостами был поставлен вопрос, можно ли совершить по ним прогулку так, чтобы пройти по каждому из этих мостов, причем ровно по одному разу." (Из книги Г.Фляйшнер Эйлеровы графы и смежные вопросы) |
| Задания дискретной математике для С12-02 |
|---|
Команды Maple теории графов. Хроматический полином Хроматический полином (Maple) Теорема о числе остовов в полном графе С12-02 Успеваемость Экран успеваемости, правила сдачи работ, содержание работ. Замечание. Большинство студентов с12-02 решило задачу о назначениях простым перебором. Напоминаем, что задания выдаются студентам для того, чтобы они освоили алгоритм (в данном случае алгоритм Куна), а не потому что преподавателя интересует ответ в задаче. Простой перебор - прямой путь к провалу на экзамене. Помните опыт предшественников, изучайте венгерский алгоритм. |

С.А.Коробков (о графах систем линейных уравнений и др.) |
 к экзамену по дискретной математике
к экзамену по дискретной математике
Защита бакалаврских работ 23.6.2005 (МЭИ, каф.теор.мех. и мехатроники)


|

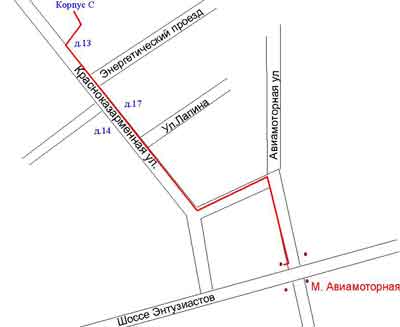
 Лефортово, Москва -2005. Ул. Авиамоторная |
 Реконструкция станции Новая моск.ж.д. июль 2005 |
 Лефортово, Москва -2005. Ул. Красноказарменная |
 кафедры теоретической механики и мехатроники МЭИ(ТУ)
кафедры теоретической механики и мехатроники МЭИ(ТУ)
